Terminal Velocity
Activity Information
Learning Goals
- $\Sigma F = 0$ does not mean no motion
- Relationship between terminal velocity and net force
- Use a computer simulation to model the impact of proposed solutions to a complex real-world problem with numerous criteria and constraints on interactions within and between systems relevant to the problem HS-ETS1-4
- Analyze data to support the claim that Newton's second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its accelerations HS-PS2-1
- Assessment Boundary: limited to one-dimensional motion and to macroscopic objects moving at non-relativistic speeds
Prior Knowledge Required
- Newton's second law of motion
- Drag equation
- $D=\dfrac{1}{2}C\rho v^2A$
- Terminal velocity
- $v=\sqrt{\dfrac{2W}{C\rho A}}$
- Gravitational force
Code Manipulation
- Copying/pasting code
- Creating code from scratch
- Translating equations into code
- While loops and if statements
—-
Activity
Handout
 Terminal Velocity
Terminal Velocity
A coin is being dropped from the top of a building. When will it reach terminal velocity? How does the force of gravity compare to the force of air resistance? Take a look at the unfinished code and answer the following questions:
Pre-coding Questions
- Create a graph showing how you think the velocity of the coin will change over time
- Create a graph showing how you think the forces of gravity, air resistance, and net force change as the coin approaches the ground.
- Using information provided by the code, calculate the terminal velocity of the falling coin. Label each part of the terminal equation, including units.
Now with your group, complete the provided code. Be sure to include arrows showing the magnitude of forces acting on the coin. As well, create a velocity vs. time graph and a forces vs. time graph (Pre-coding Questions 1 and 2). When your code is complete, answer the following questions:
Post-coding Questions/Reflection
- Describe your contributions to the coding process within your group.
- What did you find the terminal velocity to be based on the graph produced by the code? Does this agree with your calculations?
- Reflect on your predicted graphs. Explain how they were similar/different than your coding graphs. Revise your graphs as needed.
Code
Link
Answer Key
Handout
Pre-coding Answers
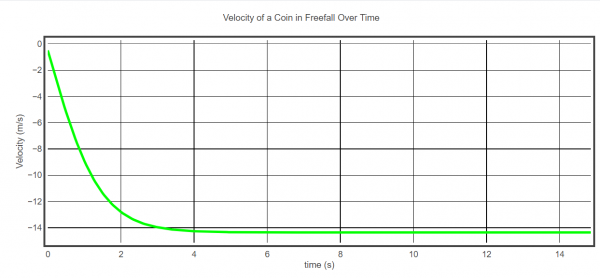
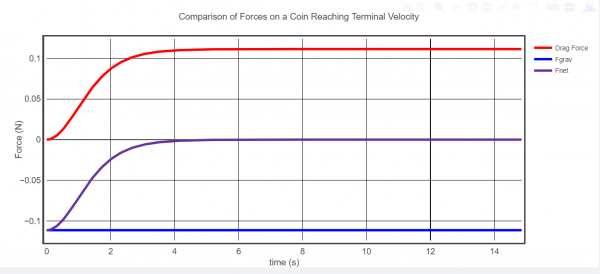
- The equation for terminal velocity is $v=\sqrt{\dfrac{2W}{C\rho A}}$, where
- $W$ is the weight of the coin (N)
- this is calculated by multiplying the mass of the coin by the acceleration of gravity: $W= 0.01135 \text{kg} * 9.81 \text{m/s/s} = 0.111 \text{N}$
- $C$ is the drag coefficient (1.15, no units)
- $\rho$ is the density of air (1.2754 kg/m³)
- $A$ is the area of the coin
- this is calculated by squaring the radius of the coin and multiplying it by pi: $A= (0.015305 \text{m})^2 * \pi = 0.000736 \text{m²}$
- $v=\sqrt{\dfrac{2*0.111}{1.15*1.275*0.000736}}=14.3 \text{m/s}$
Post-coding Answers
Use the previous answers and the completed code below to guide your reflection.
Code