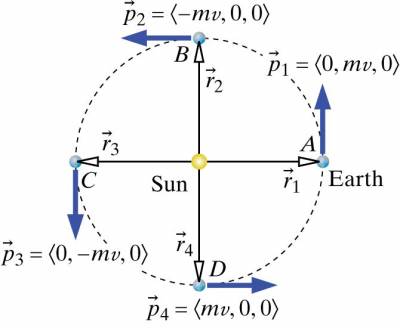
Example: Earth's Translational Angular Momentum
Calculate the magnitude of the Earth's translational (orbital) angular momentum relative to the Sun when the Earth is at location A and when the Earth is at location B as displayed in the representation of the situation in the representations. The mass of the Earth is $6$ x $10^{24}kg$ and its distance from the Sun is $1.5$ x $10^{11}m$.
Facts
Mass of the Earth: $6$ X $10^{24}$kg
Distance from the Sun: $1.5$ x $10^{11}$m
Lacking
The magnitude of the Earth's translational (orbital) angular momentum relative to the Sun when the Earth is at location A on the representation and when it is at location B on the representation.
Approximations & Assumptions
Assume Earth moves in a perfect circular orbit
Assume main interaction is with the sun
Representations
Circumference of a circle = $2\pi r$
$\vec{p} = m\vec{v}$
$v = s/t$
$\left|\vec{L}_{trans}\right| = \left|\vec{r}_A\right|\left|\vec{p}\right|\sin \theta$
Solution
The Earth makes one complete orbit of the Sun in 1 year, so you need to break down 1 year into seconds and know that the distance the Earth travels in that time is $2\pi r$ in order to find its average speed is:
$v = \frac{2\pi(1.5 \times 10^{11}m)}{(365)(24)(60)(60)s} = 3.0 \times 10^4 m/s$
With this average velocity we can find the momentum of Earth at location A as we know the mass of the Earth and now know the velocity of the Earth.
$ \vec{p} = \langle 0, 6 \times 10^{24}kg \cdot 3.0 \times 10^{4} m/s, 0 \rangle $
Computing for momentum we get:
$ \vec{p} = \langle 0, 1.8 \times 10^{29}, 0 \rangle kg \cdot m/s$
$\mid\vec{p}\mid = 1.8 \times 10^{29} kg \cdot m/s$
We know that the magnitude of the Earth's translational angular momentum relative to the sun is given by $\left|\vec{L}_{trans,Sun}\right| = \left|\vec{r}_A\right|\left|\vec{p}\right|\sin \theta$
$\mid\vec{L}_{trans,Sun}\mid = (1.5 \times 10^{11} m)(1.8 \times 10^{29} kg \cdot m/s) sin 90^{\circ}$
Compute for $\left|\vec{L}_{trans,Sun}\right|$ by inputting the known values for the variables.
$\mid\vec{L}_{trans,Sun}\mid = 2.7 \times 10^{40} kg \cdot m^2/s$
It turns out that at location $B, \mid\vec{r}\mid, \mid\vec{p}\mid$, and $\theta$ are the same as they were at location A, so $ \mid\vec{L}_{trans,Sun}\mid$ also has the same value it had at location A.