Example: Calculating the change in momentum
In another example, we determined the net force acting on the fan cart in the video below.
Now, you want to determine the change in momentum of the fan cart over a 4.2 second interval.
Setup
You need to compute the momentum change of the fan cart using the information provided and any information that you can collect or assume.
Facts
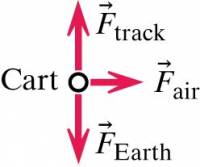
- The fan cart accelerates to the right.
- The fan cart experiences several forces including:
- the force of the air on the blades (to the right)
- the gravitational force due to the interaction with the Earth (directly downward)
- the force applied by the track (directly upward)
- a frictional forces and air resistance that resist the motion
- The acceleration due to gravity is 9.8 ms2 and is directed downward.
- In another example, we determined the net force acting on the fan cart to be, →Fcart=⟨0.45,0,0⟩N.
Lacking
- The mass of the fan cart is not given, but can be found online (mcart=0.3kg).
- The force that the air exerts on the fan blades, which is responsible for the force to right, is unknown. This could be determined by finding the change in momentum of the fan cart over some time interval. Let's say that was done and it was found to be Fair=0.45N.
Approximations & Assumptions
- Over the interval that we care about it, we will assume the net force is doesn't change. That is, the cart experiences constant force motion.
Representations
- The forces acting on the fan cart (the system's interactions with its surroundings) are represented in this free-body diagram.
- The net force acting on the fan cart is the sum of all the forces, →Fnet=∑→Fi=⟨0.45,0,0⟩N.
- The change in momentum is equal to the impulse delivered by the net force and is given by: Δ→p=→FnetΔt.
Solution
We simply compute the change in momentum from the net force and the time interval,
Δ→p=→FnetΔt=⟨0.45,0,0⟩N(4.2s)=1.89Ns
.