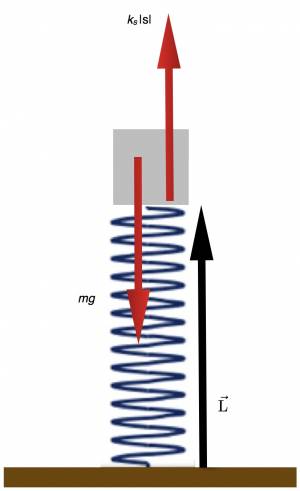
Example: Predicting the motion of a system that is subject to a spring interaction/Predicting the final location of an object moving under a non-constant force
A spring has a relaxed length of (0.2m) and it has a spring constant of 8 N/m. Attached to the top of the spring is a block of mass (.06)kg. A force is exerted on the block to compress the spring to a total length of (0.1m). Predict the y position for the block after 0.1 second and 0.2 seconds.
Facts
- Spring has relaxed length of (0.2m) $L_0=0.2m$
- Spring has compressed length of (0.1m) $|\vec{L}| = 0.1m$
- Spring has spring constant of $8 N/m$
- Block of mass (.06)kg attached to top of the spring
- The block has no initial momentum, $\vec{p_i} = \langle 0,0,0 \rangle$
- There are two forces acting on the spring, the gravitational force and the spring force
Lacking
- The $y$ position of the block after 0.1 and 0.2 seconds.
Approximations & Assumptions
- Assume block is at rest when released from compressed position therefore the initial momentum of block is zero
- Assume that the origin is at the base of the spring
- Over the time interval investigated drag forces are negligible.
Representations
- The force of the spring is given by $\vec{F}_{spring} = -k_s (|\vec{L}| - L_0) \hat{L}$
- The gravitational force is given by $\vec{F}_{Earth}=-mg$
- The momentum of the system is given by $\vec{p_f}=\vec{p_i}+\vec{F_{net}} \Delta t$
- Momentum equation = $m(\vec{v}) = \vec{p}$
- Postion update = $\vec{r_f} = \vec{r_i} + \vec{v}_{avg} \Delta t$
Solution
To solve this problem we must first set-up force equations for both spring and force due to gravity. To begin this process we must first determine the position vector ($\vec{L}$) of the mass and the length of the position vector ($|\vec{L}|$).
$$\vec{L}=\langle 0,0.1,0 \rangle - \langle 0,0,0 \rangle = \langle 0,0.1,0 \rangle m$$
$$\vec{|L|}=0.1$$
These can be used to compute the unit (direction) vector for the stretch ($\hat{s}$) (the difference between $|\vec{L}|$ and the relaxed distance \langle 0,.2,0 \rangle, which is in the same direction as the position vector.
$$\hat{L}=\langle 0,1,0 \rangle$$
As expected it is acting only in the y direction.
You can now input the unit vector and rewrite the representation for the spring force equation so that it is acting solely in the y direction as indicated by the unit vector.
$$F_{spring} = -k_s(|\vec{L}|-L_0)\langle 0,1,0 \rangle = \langle 0,-k_s(|\vec{L}|-L_0),0 \rangle$$
We know that the force due to gravity acts solely in the y direction also so we can write the representation for the force equation to represent this:
$$F_{Earth} = \langle 0,-mg,0 \rangle$$
The initial momentum of the block is zero, since you approximate that it is at rest when you release it
$$\vec{p_i}= \langle 0,0,0 \rangle$$
All of the forces acting on the system by the spring and gravitational force are in the y direction, and the initial x and z components of the blocks momentum are zero, so we only need to consider the y components of forces.
$$F_{spring} = -k_s(|\vec{L}|-L_0)\hat{L}$$
$$F_{Earth}=-mg$$
The addition of these two forces is the net force acting on the system:
$$F_{net,y} = F_{spring,y} + F_{Earth,y}$$
We needed the net force in order to be able to calculate the momentum at different time intervals as the momentum of a system is dependent on the net force on that system:
$$\vec{p_f}=\vec{p_i}+\vec{F_{net}} \Delta t$$
So we are now going to calculate the y position of the system for 0.1 seconds.
As found earlier:
$$\vec{|L|} = 0.1m$$
The stretch is equal to \vec{|L|} - the relaxed distance (0.2m).
$$s = 0.1m - 0.2m = -0.1m$$
Compute the value of the force of the spring.
$$F_{spring_y} = -8N/m(-0.1m)= +0.8N$$
Compute the value of the force due to gravity.
$$F_{Earth,y} = -0.06kg * 9.8N/kg = -0.588N$$
Add the force of spring to force due to gravity to obtain the net force.
$$F_{net,y} = .212N$$
Input this net force into the equation for momentum using 0.1s as the time to find the momentum at this instance.
$$p_{fy} = 0 + (.212N)(0.1s)\quad(Momentum\ Principle)\\$$
Compute momentum:
$$p_{fy} = 0.0212 kg * m/s$$
In order to find the change in position of the system we must find the velocity of the system for the time interval of 0.1s using the momentum just computed. Assume v_{avg,y} is approximate to v_{fy} for the time period of 0.1s.
$$v_{avg,y} \approx v_{fy}$$
Using the equation $m(\vec{v}) = \vec{p}$ we can calculate $v_{fy}$ using momentum just found and the mass of the system.
$$v_{fy} = \dfrac{p_{fy}}{m} = \dfrac{0.0212 kg * m/s}{0.06kg} = +0.353m/s$$
Using the position update equation $\vec{r_f} = \vec{r_i} + \vec{v}_{avg} \Delta t$ we can compute the new position of the system:
$$y_f = 0.1m + (0.353m/s)(0.1s) \quad(position\ update)\\$$
$$y_f = 0.135m \quad(position\ in\ y\ direction\ after\ .1s)\\$$
For the time of 0.2s we just have to repeat the process but use the new values for \vec{|L|}, s, F_{spring_y} and F_{net,y}.
Use the y position of the system for 0.1 seconds as the initial position for 0.2s.
$$\vec{|L|} = 0.135m$$
Compute the new s based on this new \vec{|L|}
$$s = 0.135m -0.2m = -0.0647m$$
Calculate the new force of the spring based on the new s distance. The force due gravity remains the same.
$$F_{spring,y} = +0.520N$$
Add the force due to the spring to the force due to gravity.
$$F_{net,y} = -0.0707N$$
Calculate the momentum using this new net force.
$$p_{fy} = (0.0212 kg * m/s) + (-0.0707N)(0.1s)$$
$$p_{fy} = 0.0141 kg * m/s$$
Calculate the new $v_{fy}$ based on this new momentum.
$$v_{fy} = 0.236 m/s$$
Update position based on this new velocity.
$$y_{f} = 0.159m \quad(position\ in\ y\ direction\ after\ .2s)\\$$
If you wished to calculate to position after 0.3s you repeat the same calculations again based on the y position that was computed for .2s.