You have read that the moment of inertia for a system of discrete particles (that rotates about its center of mass) can be calculated by adding up the product of each mass and the square of the distance from the center of mass.

$$I = \sum_i m_i r_{\perp i}^2 = m_1 r_{\perp 1}^2 + m_2 r_{\perp 2}^2 + m_3 r_{\perp 3}^2 + \dots$$

As you consider a continuous system where the particles cannot be discretized, but instead form a continuous system, the masses of the constant bits can be thought of as getting smaller and smaller. In this case, the sum becomes the integral over the whole system,

$$I = \int r^2\,dm$$

where $r^2$ is square of the magnitude of the vector that locates each bit of mass with respect to the rotation axis (typically, the center of mass). This is can be a difficult integral to perform and many tables of moments of inertia exist for typical geometric shapes and different centers of rotations. A fairly complete one appears here.

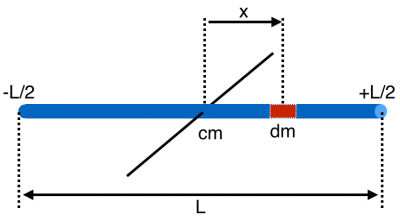
Consider a rod of length $L$ and mass $M$ that will be spun around its center of mass (figure above). The rod has a uniform mass density, so that each little chunk of rod that is the same length has the same mass. You want to calculate the moment of inertia for this rod.

The integral that defines this calculation is,

$$I = \int_{\mathrm{whole\:rod}} r^2\,dm$$

If you assume the rod is much thinner than it is long, you only have to worry about adding up the bits of mass along its length. So you end up with the one-dimensional integral,

$$I = \int_{-L/2}^{+L/2} x^2\,dm$$

What's this little $dm$? It's the little bit of mass that exists are some arbitrary location $x$. It is of length $dx$ and therefore it's mass is,

$$dm = \dfrac{M}{L}dx$$

Using this information, you can rewrite the integral,

$$I = \int_{-L/2}^{+L/2} x^2\,\dfrac{M}{L}dx = \dfrac{M}{L} \int_{-L/2}^{+L/2} x^2\,dx$$

The integral is then calculated to find the momentum of inertia for the rod about its center,

$$I = \dfrac{M}{L} \int_{-L/2}^{+L/2} x^2\,dx = \dfrac{M}{L} \dfrac{x^3}{3}\Big|_{-L/2}^{+L/2} = \dfrac{M}{3L}\left[\left(\dfrac{L}{2}\right)^3 - \left(\dfrac{-L}{2}\right)^3\right]$$ $$I = \dfrac{M}{3L}\left[\dfrac{L^3}{8} + \dfrac{L^3}{8}\right] = \dfrac{M}{3L}\dfrac{2L^3}{8} = \dfrac{1}{12}ML^2$$

which is precisely the moment of inertia of a rod about it's center.