Suggested guidelines for working through a project
Tuesday Session
Suggested approach
Read the problem individually.
One group member reads the problem out loud.
Designate one of the whiteboards as the planning board.
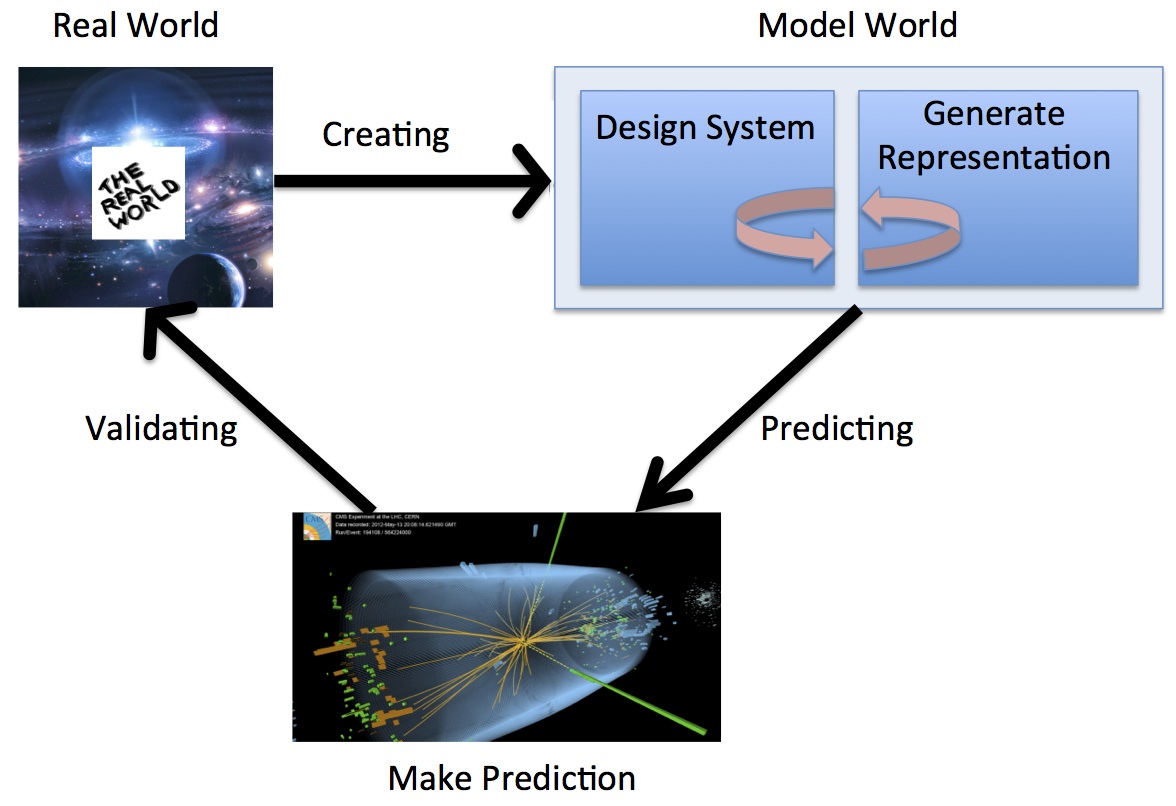
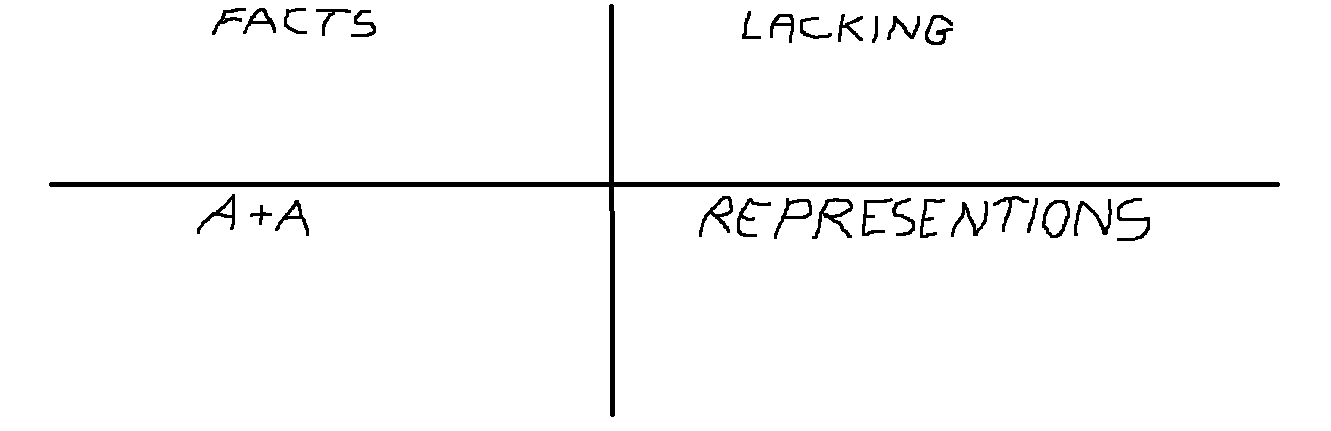
Split the planning board (see example below) into four sections:
- Facts: What information do you have? (Real World)
- Lacking: What information you need to solve this problem and how might you collect evidence to obtain this information? (Model World)
- A+A: What approximations and assumptions can you make? (Design System)
- Representations: What representations can you generate to help you understand and solve the problem. (Generate Representation)
Once you feel the planning board is complete construct a useable model world to formulate a plan to solve the problem on other whiteboard (Predicting).
The plan should include:
- What is the key idea or concept behind the problem?
- What steps must be taken to solve the problem?
Calculate answer based on plan and model world (Make a prediction).
Test this prediction against the real world (Validating):
- Does it make sense or is it reasonable?
If model is not validated reflect on model world created and restart modeling process.
For the last 5 minutes of the session generate learning issues and tasks for each group member to investigate and return to the group to explain for the next session.
Thursday Session
Spend the first 10 minutes presenting learning issues from previous day to group
Read the problem individually.
One group member reads the problem out loud.
Download and open initial code
Save the initial version of the program before you begin to play with it.
Designate one of the whiteboards as the planning board.
Split the planning board into four sections as before, you will have to interpret the given code (by playing with it) to fill in the four sections:
- Facts: What information do you have? (Real World)
- Lacking: What information you need to solve this problem? (Model World)
- A+A: What approximations and assumptions can you make and how might you collect evidence to obtain this information?? (Design System)
- Representations: What representations can you generate to help you understand and solve the problem. (Generate Representation)
Once you feel the planning board is complete construct a useable model world to formulate a plan to solve the problem (Predicting).
The plan should include:
- What is the key idea or concept behind the problem?
- What steps must be taken to solve the problem?
Calculate answer based on plan and model world (Make a prediction).
Test this prediction against the real world (Validating):
- Does it make sense or is it reasonable?
If model is not validated reflect on model world created and restart modeling process.