Defining A System
Choosing a system is one of the most important choices you make (either explicitly or implicitly) when investigating a physical situation. What we define as our physical system of interest tells us what we intend to focus on, which quantities the we might expect to be conserved, and which ones we expect to be influenced by external agents. For solving physics problems, what you define as “inside” and “outside” the system will influence the physical quantities that you are solving for, how you set up your equations, and how you model the situation. While you are free to define your system as you wish, there are often certain choices of system(s) that will make your calculations easier or more efficiently use the information you are given. In fact, some choices of system will make certain situations very difficult to model or some problems impossible to solve. Being explicit about your choice of system and how that influenced your choices and resulting solution also ensures that everyone understands what work you've done.
Lecture Video
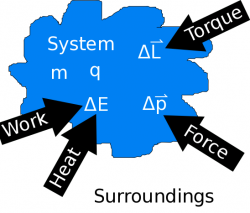
The System
The system is the object or the collection of objects that you are interested in (usually to describe its motion, explain why it follows some path, etc.). A system has various physical quantities associated with it: mass, energy, momentum, angular momentum, and entropy. These quantities can change for a system by interacting with the surroundings.
In mechanics, it was common to pick the object that is in motion as your system because you are primarily interested in describing that motion or how that motion is changing. Your job in mechanics was to predict or explain the motion of objects. In E&M, the choice of system can be a bit more nuanced. You are still interested in choosing a system that helps you predict or explain something about the system, but what that something is can be motion, energy, or something altogether new - like a field or circuit.
When we refer to a quantity as “internal,” we are referring to something that is inside the system we chose.
The Surroundings
The surroundings contain everything that you are not interested in describing. Objects that are in the surroundings can certainly influence or interact with the system, but generally, you are not interested in describing the impact of the system on the surroundings.
For example, if you drop a ball, you are typically very interested in describing how the ball's motion changes: it speeds up, gets closer to floor, it experiences a gravitational force from the Earth, etc. However, you do not talk about how the Earth's motion changes because you dropped the ball (largely because these changes are so small that they are negligible). In this case, we would choose the ball as the system and the Earth as the surroundings. This choice of system would also have implications for how to solve for the ball's final speed.
When we refer to a quantity as “external,” we are referring to something that is outside the system we chose therefore it is in the surroundings.
Implications of Defining a System
Choosing your system has particularly large implications for the 3 Fundamental Principles of Mechanics and how you set up your equations:
- If you choose your system so that there are no external forces on the system, then momentum is conserved for that system. (This is particularly relevant for collisions.)
- If you choose your system so that there is no external work or heat transferred, then energy is conserved for that system. (This can very much simplify the discussion of complex phenomenon.)
- If you choose your system so that there is no external torque on the system, then angular momentum is conserved for that system. (This is also particularly important for collisions.)