Section 21.3 from Matter and Interactions (4th edition)
Putting Gauss's Law Together
At this point, we have talked about how to find the electric flux through flat surfaces and through curved surfaces as well how to find the enclosed charge using charge density. These notes will go through two examples of how we find the electric field at a single point using electric flux, enclosed charge and symmetry arguments (Gauss's Law). You should notice many similarities between the steps that we use for Gauss's Law and those that we used for Ampere's Law. Finally, we will discuss the advantages/disadvantages to using Gauss's Law.
Line of charge example
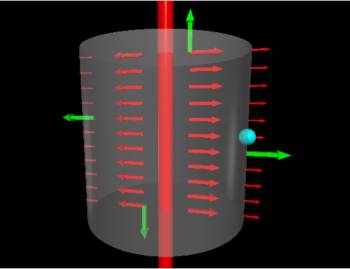
Suppose we want to find the electric field at Point P (shown by the teal dot), which is a distance of $d=.05 m$ away from a very long line of charge (shown by the red line) with a charge density of $\lambda=4\:nC/m$. Instead of building up the electric field by splitting the line into chunks, we will use the symmetry of the line charge to solve Gauss's Law. Remember Gauss's Law says that the total electric flux through a closed Gaussian surface must be equal to the amount of charge (divided by a constant) inside the Gaussian surface. $$\Phi_{tot}=\int \vec{E} \bullet \vec{dA}=\frac{Q_{enclosed}}{\epsilon_0}$$
Step 1 - Draw the electric field lines
Assuming Point P is close to the center of a very long line of positive charge, the electric field close to the center will point radially away from the line of charge, meaning the electric field vectors (shown by the red arrows) point horizontally away from the line and are the same size for a certain distance away from the line.
Step 2 - Determine a good Gaussian surface and find the electric flux through the Gaussian surface
When we are picking our Gaussian surface, we want to pick a shape with sides that are either parallel to or perpendicular to the electric field vectors. In this case, a cylinder will work nicely. Remember that the choice of Gaussian surface is completely arbitrary, so we are picking a shape that will provide the simplest math. We will pick our cylinder to have a radius equal to $d=.05 m$, so that Point $P$ is on the edge of the cylinder. The height of the cylinder doesn't particularly matter as long as it is small enough to not include the end points of the line, so let's just call the height of the cylinder $h$. We will want the center of the cylinder to be centered along the line of charge so that the electric field along the surface of the cylinder is constant in direction and magnitude.
Now that we have a Gaussian surface, we can find the electric flux at the surface of the cylinder. The cylinder has three surface - the flat top, the flat bottom, and the curved side of the cylinder - so we need to account for the flux through all three surfaces to find the total electric flux. $$\Phi_{tot}=\int \vec{E}_{top} \bullet \vec{dA}_{top}+ \int \vec{E}_{bottom} \bullet \vec{dA}_{bottom}+\int \vec{E}_{side} \bullet \vec{dA}_{side}$$ Starting with the top surface, the electric field vectors would still be pointing radially away from the line of charge (since we are still in the middle of the line of charge) and the area vector (shown by the green arrow) for the top surface would point perpendicularly away from the top surface (up in this case). This means at every location on the top surface, the electric field vectors would be perpendicular to the dA vectors so the dot product for the top surface is zero: $$\Phi_{top}=\int \vec{E}_{top} \bullet \vec{dA}_{top} = 0$$ Similarly for the bottom surface, the electric field vectors point radially away from the line of charge, but the dA vectors (shown by the green arrow) would point down (perpendicular to the surface). So the electric flux through the bottom surface is also zero. $$\Phi_{bottom}=\int \vec{E}_{bottom} \bullet \vec{dA}_{bottom} = 0$$ These answers should make sense since there are no electric field lines that poke through the top or bottom surfaces of the Gaussian cylinder.
This leaves the electric flux through the side of the cylinder. We know that the electric field points radially away from the center of the line. Since we have circular cylinder, any dA along the curved side (shown by the green arrows) would also point radially away from the surface. Thus, for any point along the side of the cylinder, the electric field vector and the dA vector would be parallel. This means the dot product reduces to a simple multiplication of the magnitudes. $$\Phi_{side}=\int \vec{E}_{side} \bullet \vec{dA}_{side} = \int |\vec{E}_{side}| |\vec{dA}_{side}| cos(0)$$ $$\Phi_{side}=\int E_{side} dA_{side}$$
Since the side surface of the cylinder is the same distance away from the line of charge, the magnitude of the electric field is constant at every point along the side. This means that E is constant over the whole surface area, so we can pull it out of the integral. $$\Phi_{side}=E_{side} \int dA_{side}$$ Then the integral of dA is just A (or rather adding up all the little pieces of area gives you the total area). $$\Phi_{side}=E_{side}A_{side}$$ We can then rewrite the surface area of the side of the cylinder in terms of the radius of the cylinder (d) and the height of the cylinder (h). $$\Phi_{side}= E_{side} 2\pi d h$$ So including the fact that the electric flux through the top and bottom of the cylinder, we get the total electric flux to be: $$\Phi_{tot}= E_{side} 2\pi d h$$
Step 3 - Find the amount of charge enclosed
Now, we need to figure out how much charge is enclosed by the Gaussian cylinder that we chose. Since we said that the height of the cylinder was h, then we can use the given charge density to determine the enclosed charge: $$Q_{encl} = \lambda l = \lambda h$$ Checking the units shows that we have $C = \frac{C}{m}m$, which is the charge that we are trying to find.
Step 4 - Solve for electric field and determine the direction
Now we can plug the total electric flux and the enclosed charge into Gauss's Law, then solve for the electric field: $$\Phi_{tot}= \frac{Q_{enclosed}}{\epsilon_0}$$ $$E_{side} 2\pi d h=\frac{\lambda h}{\epsilon_0}$$ $$E_{side} =\frac{\lambda h}{\epsilon_0 2\pi d h}$$ $$E_{side} =\frac{\lambda}{\epsilon_0 2\pi d}$$ $$E_{side} =\frac{4*10^{-9}}{8.85*10^{-12}* 2\pi*0.05}=1439\:N/C$$ This is then the magnitude of the electric field anywhere along the side of the cylinder, including Point P. If we want to write the electric field vector at Point P, then we need to add the direction to the field magnitude we just found. Before (in Step 1), we already determined that the electric field would point radially away from the line of charge. So the electric field at Point P will point in the $+\hat{x}$ direction (in cartesian coordinates) or in the $\hat{r}$ direction (in cylindrical coordinates). Thus, we found the electric field at Point P to be: $$\vec{E}_P =\frac{\lambda}{\epsilon_0 2\pi d} \hat{x}$$ $$\vec{E}_P = 1439\:N/C\:\hat{x}$$
Gauss's Law Steps Summary
Thus, to summarize, the steps for using Gauss's Law are:
- Figure out and draw the electric field around the charge distribution.
- Choose a Gaussian surface that a) goes through your observation point, b) has area vectors that are either parallel or perpendicular to the electric field vectors, and c) has a constant electric field along the Gaussian surface. This allows you simplify the electric flux integral.
- Find the amount of charge enclosed by the Gaussian surface (maybe using charge density if you need a fraction of the total charge).
- Solve for the electric field and determine the direction.
Advantages and Disadvantages of Using Gauss's Law
While there are many advantages to using Gauss's Law, there are also many disadvantages to using Gauss's Law. For example, Gauss's Law is always true, but requires high levels of symmetry to actually solve for the electric field. This means that if you have a case with symmetry (points, spheres, lines, cylinders, or plates), Gauss's Law will almost always be easier to use. However, if you have a charge that is not symmetric (like almost any real word object), it is better to split the charge into dQ's and add the fields from the little chunks. It is also better to use the dQ method when you are unsure of what the electric field looks like - if you don't know this ahead of time, it is much harder to choose a Gaussian surface that will simplify your integral. Lastly, it is much easier to make computational models using the dQ method than it is with Gauss's Law.
Example
-
- Video Example: Gauss's Law Application – A Ball of Charge