Section 20.1 in Matter and Interactions (4th edition)
Path of a Charge through a Magnetic Field
We just talked about the force that a moving charge feels when it travels through a magnetic field. So now the question remains: what happens to the charge when it feels this force? Since the magnetic force is perpendicular to the velocity of the charge, we will show that the charge actually begins to move in a circular pattern.
Path of the Moving Charge
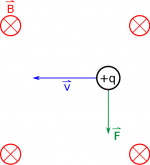
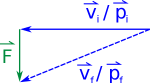
Let's start by considering a charge moving to the left ($-\hat{x}$ direction) in a magnetic field that points into the page ($-\hat{z}$ direction). Using the right hand rule, we can figure out that the force on this charge is down ($-\hat{y}$ direction). So what does this mean for the path of our charge? We can use the momentum principle to help us figure it out. The momentum principle says that: $$\Delta \vec{p} = \vec{p}_f - \vec{p}_i = \vec{F}_{net,avg} \Delta t$$ where momentum is simply $\vec{p}=m\vec{v}$ (meaning momentum points in the same direction as velocity). We can rewrite the momentum principle into it's “update form” by saying: $$\vec{p}_f = \vec{F}_{net,avg} \Delta t + \vec{p}_i$$
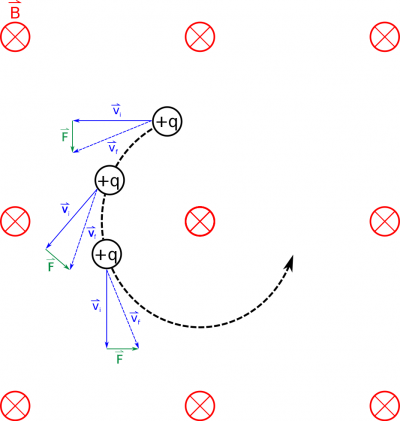
This means that if our magnetic force is pushing the charge down for a short time, the velocity of the charge will then point slightly down. If we do the same process at the next location and the next location (it turns out a computer is pretty good at doing these calculations), we find that the charge will move in a circle, with the magnetic force always pointing toward the center of the circular path. It turns out that this is a perfect example of uniform circular motion.
Work Done
You may be wondering if there is a magnetic potential energy associated with the magnetic field (after all we did use the electric force to get to electric potential energy). We can figure this out by first looking at the work done by the magnetic field on the charge. Remember that the general equation for work is given by: $$W_{total} = \int_i^f \vec{F}\cdot d\vec{r}$$ In this case, the force is the magnetic force, which we have already said points perpendicular to the path ($d\vec{r}$) at every point in the circle. $$W_{B}=\int_i^f \vec{F}_{B}\cdot d\vec{r}$$ Since the dot product is between the magnetic force and the path direction, and because those vectors are perpendicular, this tells us that the work done by the magnetic field is actually zero. $$W_{B}=0$$ This is an important result because this tells us that there is no change in the energy of the particle. In other words, the magnetic force only changes the direction of the moving charge - it does not slow down or speed up as it travels through the magnetic field (unless there is a non-magnetic force also acting on it). The magnetic field can only turn a charge not accelerate it.
This also means that we do not have a way to define a magnetic potential or a magnetic potential energy in the same way that we did with electric fields. It turns out that we can define a vector potential, which you may talk about in your future courses.
Examples
-
- Video Example: Helical Motion in a Magnetic Field