Marshmallow Launch

Activity Information

Learning Goals

• Create and modify a computational model to describe a given system
• Use Newton’s second law to relate the acceleration of a marshmallow with the forces acting on it (HS-PS2-1)

Prior Knowledge Required

• Vectors
• Kinematics in 2d
• Drag force equation

Code Manipulation

• Interpret existing code
• Edit existing code
• Create new code from mathematical equations
• Copy / Paste code

Activity

Handout – Marshmallow Launch

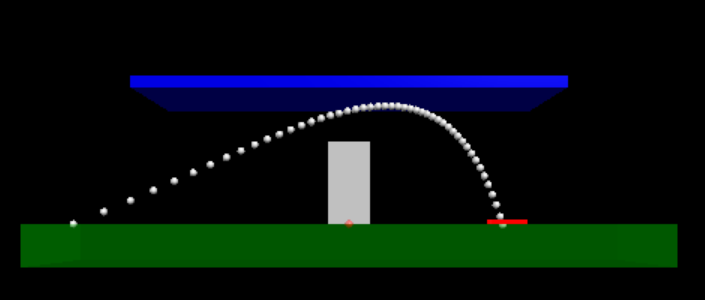
The bi-annual marshmallow launch is a definitely real and highly important tradition in Michigan. It consists of many teams creating small catapults to launch marshmallows over an obstacle, onto a target. Additionally, there is a ceiling that the teams must also avoid.

You’ve gathered a team to enter this year’s marshmallow launch. You’ve decided that the best way to get ahead of your competition is to create a computer simulation of the launch, so you can test many different initial velocities and launch angles of the marshmallow.

This is what you have so far. (click “remix” to save your own version)

Your simulation should accurately show the motion of a marshmallow once it has been launched. It should also stop if the marshmallow hits the ground, the ceiling, or the obstacle. Finally, it should also produce a graph of the x and y velocities of the marshmallow vs time.

Once you get your simulation working, add air resistance to it. How does this effect what initial velocity is required?

The coefficient of drag between the marshmallow and air is 0.2 and its reference area is 0.0025 m^2

Code

Link

GlowScript 2.7 VPython
#setting the scene - these can be changed as necessary for your screen size
scene.width = 500
scene.height = 600

#define some variables
test = 0                #condition test
g =  -10                 #Gravitational Field Strength - in N/kg
dt = 0.0001             #time increment
mass = .0015            #marshmallow mass in kg
mmvelocity = vec(0,0,0) #set initial value of variable
t = 0                   #set initial value of variable

#defining the objects
ground = box(pos = vector(0,-.5,0),length=15, height=1, width=4, opacity = .3,color=color.green)      #the floor - floor surface is at 0.5m
ceiling = box(pos = vector(0,3.25,0),length=10, height=.25, width=4, color=color.blue)                #the ceiling - bottom of the ceiling is 2.5m above floor
mm = sphere(pos = vector(-7,0, 0), radius=0.1, color=color.white, make_trail = True, trail_type = "points", trail_radius = .1, interval = 300, velocity = vec(0,0,0))  #marshmallow
center = sphere(pos = vec(0,0,0), radius = 0.1, color = vec(1,0,0))                                  #location of point 0,0,0
launchline = box(pos = vec(-4,0,0), length = 0.05, width = 4, height = 0.01, color = vec(1,.5,0))
obstacle = box(pos = vec(0,1,0), length=1, height=2, width=2, opacity = .5, color=vec(50,5,50))      #obstacle
target = cylinder(pos=vec(4,0, 0),radius=.5, axis = vec(0,.125,0), color=vec(150,0,0))               #target - 8 meters from launch location

# define graph of motion
grph = graph(title='Change Me!!', xtitle='Change Me!!', ytitle='Change Me!!')
mmgraph1 = gcurve(color=color.red,  markers=True, marker_color=color.red, width = 5, label="Hi, I'm Red!")
mmgraph2 = gcurve(color=color.blue,  markers=True, marker_color=color.blue, width = 5, label="Hi, I'm not Red!")

#marshmallow launch parameters
launchvelocity = 10.5                              #launch speed of marshmallow
launchangle = 45                                   #launch angle in degrees
launchanglerad=launchangle*3.14/180                #change launch angle to radians
mmvelocity.x = launchvelocity*tan(launchanglerad)  #horizontal component of launch velocity - this might not be right

#loop to create the animation
while test == 0:
    rate(1000)

    if mm.pos.y < ground.pos.y + 0.50:  #check to see if the marshmallow has hit the ground
        test = 1
           
    t = t+dt                            #increment the time
    
    #mmgraph1.plot(t, mmvelocity.x)        #graph of horizontal velocity vs time
    #mmgraph2.plot(t, mmvelocity.y)        #graph of vertical velocity vs time 

Answer Key

Handout

First, the initial velocity of the marshmallow needs to be broken into its components. To do this, we can construct a triangle that’s hypotenuse is the initial velocity of the marshmallow:

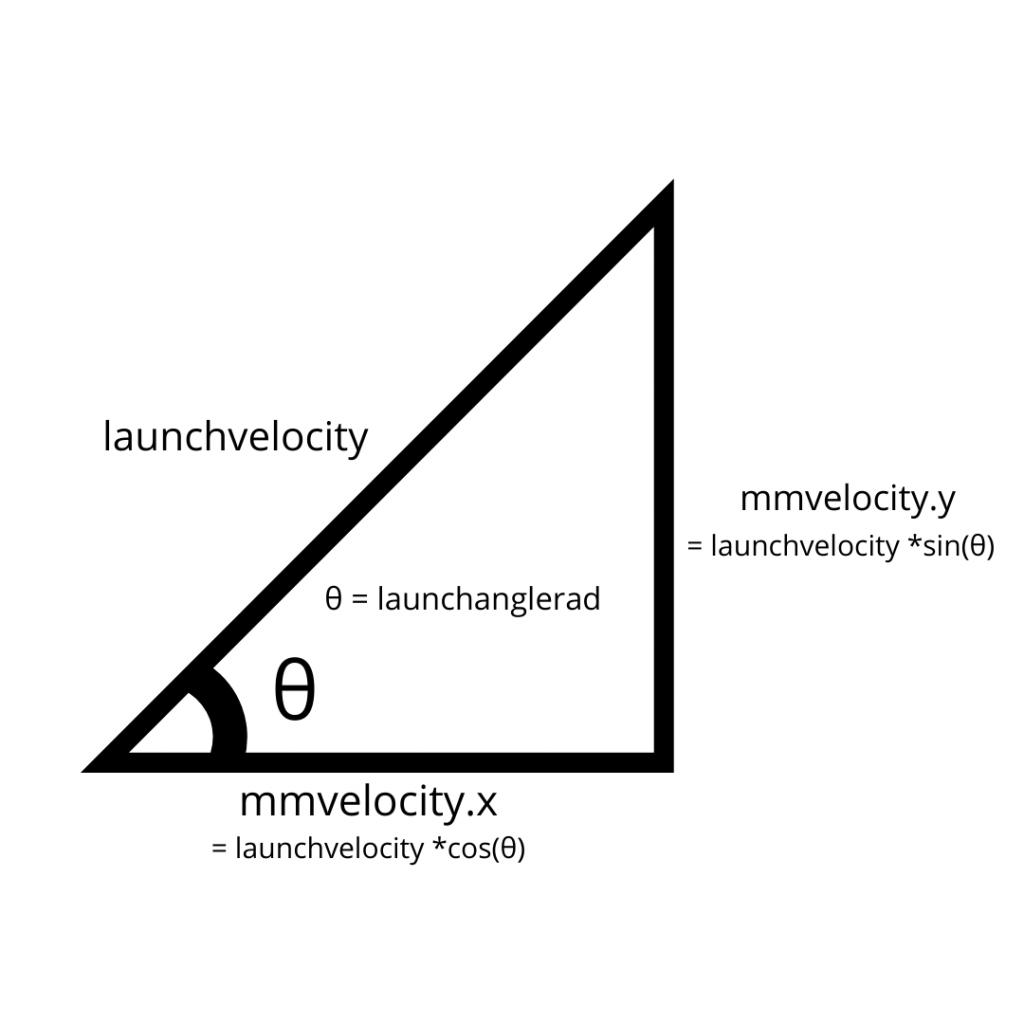
Now this can be implemented into the code, noting that the marshmallow’s initial velocity in the z-direction is zero:

launchvelocity = 30      #launch speed of marshmallow
launchangle = 21         #launch angle in degrees
launchanglerad=launchangle*3.14/180    #change launch angle to radians

mmvelocity.x = launchvelocity*cos(launchanglerad)  #horizontal component of launch velocity
mmvelocity.y = launchvelocity*sin(launchanglerad)  #vertical component of launch velocity
mmvelocity.z = launchvelocity*0   #z - direction initial velocity                                                             

Now we can add the force of gravity and initialize the net force. This can happen outside of the while loop because the gravitational force can be approximated to be constant near earth.

t = 0                   #set initial value of variable
Fg = mass * g           #earth force on marshmallow
Fgrav = vec(0,Fg,0)     #vector for earth force on marshmallow
Fnet = vec(0,0,0)       #initialize net force vector

Now that these have been initialized, they can be used in the while loop to find the acceleration of the marshmallow:

while test == 0:
    rate(1000)

    if mm.pos.y <= ground.pos.y + 0.49:    #check to see if the marshmallow has hit the ground
        test = 1
  
    Fnet = Fgrav        #calculate the net force on the marshmallow - gravity is the only force acting on it until air resistance is accounted for

    mmaccel = Fnet/mass #update the acceleration, comes from Fnet = ma

Now we need to make it so the model will stop running if the marshmallow hits the ceiling or the obstacle. To do this, more if statements similar to the one that checks to see if the marshmallow has hit the ground can be added:

while test == 0:
    rate(1000)

    if mm.pos.y >= ceiling.pos.y - 0.175:  #check to see if the marshmallow has hit the ceiling
        test = 1
    
    if mm.pos.y < 2.05 and mm.pos.x > -1.05 and mm.pos.x < 1.05: #check to see if the marshmallow has hit the obstacle
        test = 1

Now the graph labels need to be changed to something more sensible. Many different labels are appropriate, this solution opts for the following:

grph = graph(title='Velocity vs Time', xtitle='Time (s)', ytitle='Velocity (m/s)')
mmgraph1 = gcurve(color=color.red,   width = 5, label='Horizontal')
mmgraph2 = gcurve(color=color.blue,   width = 5, label='Vertical')

The lines of code that update the graph in the while loop also need to be un-commented.

This completes the problem without factoring in air resistance. Changing the values of launchvelocity and launchangle changes the initial conditions.

In order to account for air resistance, more initial variables need to be added:

Cd = 0.2 #0.47              #coefficient of drag for a sphere
rho = 1.2                   #density of air
A = 0.0025                  #area of a marshmallow 5cm oer side
mmdrag = vec(0,0,0)         #initialize the drag force on the marshmallow

Now the drag force equation can be used in the while loop to find the force of drag in the x and y directions:

    mmdrag.x = -0.5 * Cd * rho * A * ((mmvelocity.x)**2)  #calculate the force of the air resistance in the horizontal direction
    mmdrag.y = -0.5 * Cd * rho * A * ((mmvelocity.y)**2)  #calculate the force of the air resistance in the vertical direction

Because a new force has been introduced, it has to be part of the net force:

     Fnet = Fgrav + mmdrag

Now the problem is solved with air resistance!

Code

Solution without air resistance:

Link

GlowScript 3.1 VPython

#setting the scene - these can be changed as necessary for your screen size
scene.width = 500
scene.height = 600

#define some variables
test = 0                #condition test
g =  -10                #Gravitational Field Strength - in N/kg
dt = 0.0001             #time increment
mass = .0015            #marshmallow mass in kg
mmvelocity = vec(0,0,0) #set initial value of variable
t = 0                   #set initial value of variable
Fg = mass * g           #earth force on marshmallow
Fgrav = vec(0,Fg,0)     #vector for earth force on marshmallow
Fnet = vec(0,0,0)       #initialize net force vector


#defining the objects
ground = box(pos = vector(0,-.5,0),length=15, height=1, width=4, opacity = .3,color=color.green)      #the floor - floor surface is at 0.5m
ceiling = box(pos = vector(0,3.25,0),length=10, height=.25, width=4, color=color.blue)               #the ceiling - bottom of the ceiling is 2.5m above floor
mm = sphere(pos = vector(-7,0, 0), radius=0.1, color=color.white, make_trail = True, trail_type = "points", trail_radius = .1, interval = 300, velocity = vec(0,0,0))  #marshmallow
center = sphere(pos = vec(0,0,0), radius = 0.1, color = vec(1,0,0))                                  #location of point 0,0,0
launchline = box(pos = vec(-4,0,0), length = 0.05, width = 4, height = 0.01, color = vec(1,.5,0))
obstacle = box(pos = vec(0,1,0), length=1, height=2, width=2, opacity = .5, color=vec(50,5,50))      #obstacle
target = cylinder(pos=vec(4,0, 0),radius=.5, axis = vec(0,.125,0), color=vec(150,0,0))               #target - 8 meters from launch location

# define graph of motion
grph = graph(title='Velocity vs Time', xtitle='Time (s)', ytitle='Velocity (m/s)')
mmgraph1 = gcurve(color=color.red,   width = 5, label='Horizontal')
mmgraph2 = gcurve(color=color.blue,   width = 5, label='Vertical')

#marshmallow launch parameters
launchvelocity = 10.5                              #launch speed of marshmallow
launchangle = 45                                   #launch angle in degrees
launchanglerad=launchangle*3.14/180                #change launch angle to radiams
mmvelocity.x = launchvelocity*cos(launchanglerad)  #horizontal component of launch velocity
mmvelocity.y = launchvelocity*sin(launchanglerad)  #vertical component of launch velocity
mmvelocity.z = launchvelocity*0                    #z - direction initial velocity


#loop to create the animation
while test == 0:
    rate(1000)

    if mm.pos.y >= ceiling.pos.y - 0.175:  #check to see if the marshmallow has hit the ceiling
        test = 1
    
    if mm.pos.y < 2.05 and mm.pos.x > -1.05 and mm.pos.x < 1.05: #check to see if the marshmallow has hit the obstacle
        test = 1

    if mm.pos.y <= ground.pos.y + 0.49:    #check to see if the marshmallow has hit the ground
        test = 1
  
    Fnet = Fgrav                          #calculate the net force on the marshmallow

    mmaccel = Fnet/mass                   #update the acceeration

    mmvelocity = mmvelocity + mmaccel*dt  #update the velocity

    mm.pos = mm.pos + mmvelocity * dt     #update the position
    
    t = t + dt                            #increment tbe time


    mmgraph1.plot(t, mmvelocity.x)        #graph of horizontal velocity vs time
    mmgraph2.plot(t, mmvelocity.y)        #graph of vertical velocity vs time  

Solution with air resistance:

Link – click “remix” to edit and view the code properly

GlowScript 3.1 VPython

#setting the scene - these can be changed as necessary for your screen size
scene.width = 500
scene.height = 600

#define some variables
test = 0                    #condition test
g = -10                     #Gravitational Field Strength - in N/kg
dt = 0.0001                 #time increment
mass = .0015                #marshmallow mass in kg
mmvelocity = vec(0,0,0)     #set initial value of variable
t = 0                       #set initial value of variable
Cd = 0.2 #0.47              #coefficient of drag for a sphere
rho = 1.2                   #density of air
A = 0.0025                  #area of a marshmallow 5cm oer side
mmdrag = vec(0,0,0)         #initialize the drag force on the marshmallow
Fg = mass * g               #earth force on marshmallow
Fgrav = vec(0,Fg,0)         #vector for earth force on marshmallow
Fnet = vec(0,0,0)           #initialize net force vector


#defining the objects
ground = box(pos = vector(0,-.5,0),length=15, height=1, width=4, opacity = .3,color=color.green)      #the floor - floor surface is at 0.5m
ceiling = box(pos = vector(0,3.25,0),length=10, height=.25, width=4, color=color.blue)                #the ceiling - bottom of the ceiling is 2.5m above floor
mm = sphere(pos = vector(-7,0, 0), radius=0.1, color=color.white, make_trail = True, trail_type = "points", trail_radius = .1, interval = 300, velocity = vec(0,0,0))  #marshmallow
center = sphere(pos = vec(0,0,0), radius = 0.1, color = vec(1,0,0))                                  #location of point 0,0,0
launchline = box(pos = vec(-4,0,0), length = 0.05, width = 4, height = 0.01, color = vec(1,.5,0))
obstacle = box(pos = vec(0,1,0), length=1, height=2, width=2, opacity = .5, color=vec(50,5,50))      #obstacle
target = cylinder(pos=vec(4,0, 0),radius=.5, axis = vec(0,.125,0), color=vec(150,0,0))               #target - 8 meters from launch location

# define graph of motion
grph = graph(title='Velocity vs Time', xtitle='Time (s)', ytitle='Velocity (m/s)')
mmgraph1 = gcurve(color=color.red,   width = 5, label='Horizontal')
mmgraph2 = gcurve(color=color.blue,   width = 5, label='Vertical')

#marshmallow launch parameters
launchvelocity = 30                                #launch speed of marshmallow
launchangle = 21                                   #launch angle in degrees
launchanglerad=launchangle*3.14/180                #change launch angle to radiams
mmvelocity.x = launchvelocity*cos(launchanglerad)  #horizontal component of launch velocity
mmvelocity.y = launchvelocity*sin(launchanglerad)  #vertical component of launch velocity
mmvelocity.z = launchvelocity*0                    #z - direction initial velocity                                                              #z - direction initial velocity

#loop to create the animation
while test == 0:
    rate(1000)

    if mm.pos.y >= ceiling.pos.y - 0.175: #check to see if the marshmallow has hit the ceiling
        test = 1
    
    if mm.pos.y < 2.05 and mm.pos.x > -1.05 and mm.pos.x < 1.05:   #check to see if the marshmallow has hit the obstacle
        test = 1

    if mm.pos.y <= ground.pos.y + 0.49:   #check to see if the marshmallow has hit the ground
        test = 1
    
    mmdrag.x = -0.5 * Cd * rho * A * ((mmvelocity.x)**2)  #calculate the force of the air resistance in the horizontal direction
    mmdrag.y = -0.5 * Cd * rho * A * ((mmvelocity.y)**2)  #calculate the force of the air resistance in the vertical direction

    Fnet = Fgrav + mmdrag                 #calculate the net force on the marshmallow

    mmaccel = Fnet/mass                   #update the acceeration

    mmvelocity = mmvelocity + mmaccel*dt  #update the velocity

    mm.pos = mm.pos + mmvelocity * dt     #update the position
    
    t = t + dt                            #increment tbe time


    mmgraph1.plot(t, mmvelocity.x)        #graph of horizontal velocity vs time
    mmgraph2.plot(t, mmvelocity.y)        #graph of vertical velocity vs time