• Develop and use models to illustrate that energy at the macroscopic scale can be accounted for as a combination of energy associated with the motions of particles and energy associated with the relative position of particles ( HS-PS3-2)
• Apply kinetic theory to state change and energy changes within matter
• Explain and visualize how the physical properties of matter change (at atomic and macroscopic levels) to an energy input or temperature change
• Plot and interpret the graph of temperature vs. time (heating curve) of a material
• Use terms that describe what is happening on each part of the curve
  • melting, condensing, boiling, etc.

• Kinetic theory of motions
• States of Matter
• Heat and Enthalpy
  • $Q = mC\Delta T$

• Copying/pasting code
• Creating code from scratch
• While loops and if statements
• translating equations into code

—-

Phase Changes

A graph of the temperature of a material over time is called a heating curve. The heating curve shows the change of state of a material as more energy (higher temperature) is added to the material. The sloped regions of the graph show how energy is raising the temperature of that state until a plateau (the flat regions of the graph) is reached. This is known as *specific heat*. Specific heat capacity (shown as the variable “$C$” — not to be confused with Celsius of Calories) is the amount of heat required to change the temperature of a mass unit of a substance by one degree. For special conditions, $C_v$ is used for isochoric (constant volume) environments or $C_p$ for isobaric (constant pressure) environments. $Q = mC\Delta T$ is the governing equation, where $Q$ is the total energy in kilojoules, $m$ is the mass of the substance in grams, and $\Delta T$ is the difference between the final and initial temperatures of the substance in Kelvin.

During the plateau, additional energy is needed to bring the entire mass of the matter to a point where it can move to the next state. This is known as the *latent heat* of the substance and is shown as the variable $L$. The total energy is given by the equation $Q=mL$.

Below is a graph showing the heating curve for water. Take a look and use the code below and then answer the following questions that investigate the relationships between kinetic energy level, temperature, particle movement, etc.

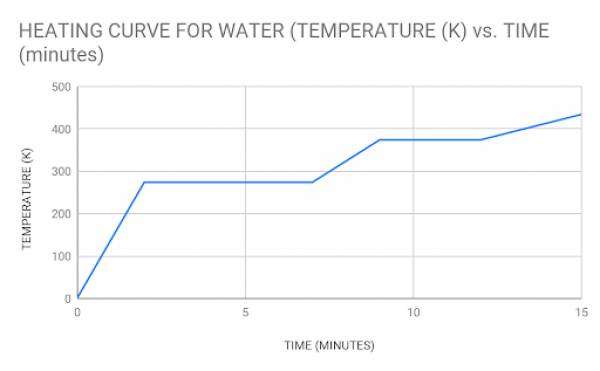
1. If the particle movement is low, the matter is in the _____ state.
2. The _____ state is reached as particles exhibit very high energy at a correspondingly _____ temperature.
3. When a gas loses so much energy it turns into a liquid, it undergoes _____.
4. Since particles in a solid are closely packed together, they can only move _____.
5. Particles exhibit _____ velocities in the highest energy state.
6. Solid particles that absorb so much energy they turn into a gas undergo _____.
7. At moderate levels of kinetic energy, the particles can move _____ and the matter exists as a _____.
8. Lower energy means _____ particle movement and _____ temperature.
9. Theoretically, no particle movement occurs at _____ °C (0 K).
10. Solids typically have _____ temperatures than gases.
11. If a gas is super heated to thousands of Kelvin, it ionizes and becomes _____.
12. Increases in _____ result in greater particle velocity and therefore greater kinetic energy.
13. The Kinetic Theory of Matter says that for hotter temperatures, the _____ of the particles move in matter.

Using the graph above, answer the following questions:

1. Partition this graph into three regions showing the 3 states of matter — label each region and shade it a different color.
2. Identify where the matter changes from one state to another.
3. Energy is increasing from left to right; label each part of the curve to describe what the matter is doing as energy increases (above the curve) and when energy is decreasing (below the curve). For example, as energy is added, what word describes how the solid changes?
4. Based on the graph, at what temperature (K) does the matter freeze?
5. At what temperature does the matter vaporize?
6. If water ionizes (and turns into plasma) at 12000 K, is this graph an accurate model of how water changes state?
7. Looking at the heating curve program, What do you notice about the first and second plateaus? what does this say about the heat capacity of water in the liquid vs. the steam state? Which state is more efficient/better for carrying heat?

Now that you understand how the program works to show the relationship between kinetic energy, particle movement, and temperature, it is time to apply your knowledge to improving and extending the power of the program. Develop answers to the following questions by modifying and improving the existing code.

1. Do you think the movement of all particles is the same for all substances given the same energy? For example, should a particle of hydrogen (mass = 1.01 amu) move at the same velocity as a particle of nitrogen (mass = 14.01 amu) for a given temperature?
2. What are some of the key equations you would need to model the movement of the particles?
3. Which variables are constants and which can change?
4. How could we show different movement for different types of substances?
5. How would the heating curve graph look if we used another substance?
6. So far, all these calculations have been isobaric (same pressure) and isochoric (same volume). What would happen to your answers if the pressure was doubles to 2 atmospheres? How would you model that? Would that affect your entire heating curve or just a portion? What equations relate pressure, temperature, and volume?

Link

GlowScript 2.7 VPython
#COLLAPSE LINES 3, 8, 11, AND 16! These are special bundles of code, called subroutines, which help simplify the coding later in the program.
def ShrinkSolidGrowLiquid():#This subroutine changes the sizes of the solid and liquid phases during melting
    solid.pos=solid.pos+vec(0,-(L_box/(2*ceil(m*Hfus/dE))),0) #SizeIncrement1=L_box/(2*ceil(m*Hfus/dE))
    solid.radius=solid.radius-(L_box/(2*ceil(m*Hfus/dE)))
    liquid.pos=liquid.pos+vec(0,0.5*(L_box/(2*ceil(m*Hfus/dE))),0)
    liquid.size=liquid.size+vec(0,(L_box/(2*ceil(m*Hfus/dE))),0)
def ShrinkLiquid():#This subroutine changes the size of the liquid phase during vaporization
    liquid.pos=liquid.pos+vec(0,-0.5*L_box/(2*ceil(m*Hvap/dE)),0) #SizeIncrement2=L_box/(2*ceil(m*Hvap/dE))
    liquid.size=liquid.size+vec(0,-L_box/(2*ceil(m*Hvap/dE)),0)
def MakeNewParticle():#This subroutine creates a new gas particle and adds it to a list of particles
    newparticle = sphere(pos=vector(L_box*(random()-0.5),(L_box-liquid.size.y)*(random()-0.5)+liquid.size.y/2,L_box*(random()-0.5)),radius=0.05, color=color.cyan)
    newparticle.mass = 1
    newparticle.velocity = vector(random()-0.5,random()-0.5,random()-0.5)*2 #the coefficient of 2 is a scaling factor for visual effect
    listOfParticles.append(newparticle)
def ParticleMovementAndCollisions(): #This subroutine moves gas particles and handles particle-wall and particle-particle collisions
    for particle in listOfParticles:
        if Etotal > Eboil: #If all the liquid has evaporated, start increasing the velocity of the gas particles
            particle.velocity=particle.velocity+sqrt(2*dE/particle.mass)*(particle.velocity/mag(particle.velocity))*2E-4 #Increase velocity with increasing energy. The coefficient of 2E-4 is a scaling factor for visual effect
        particle.pos = particle.pos + particle.velocity*0.1 #Update particle position, assume dt=0.1
        if abs(particle.pos.x) >= container.length/2:#Particle-wall collision in x
            particle.velocity.x = - particle.velocity.x
        if abs(particle.pos.y) >= container.height/2 or particle.pos.y <= (liquid.size.y-L_box/2):#Particle-wall collision in y
            particle.velocity.y = - particle.velocity.y
        if abs(particle.pos.z) >= container.width/2:#Particle-wall collision in z
            particle.velocity.z = - particle.velocity.z
    for i in range(0,len(listOfParticles)):#Particle-particle collisions, loop through every particle
        for j in range(i+1,len(listOfParticles)):#loop through every OTHER particle
            diff = listOfParticles[j].pos - listOfParticles[i].pos #displacement vector between two particles
            distance = mag(diff) #magnitude of displacement is distance
            if distance <= listOfParticles[i].radius + listOfParticles[j].radius: #if particles will collide, check their next positions
                nextpos1 = listOfParticles[i].pos + listOfParticles[i].velocity*0.1 #assume dt=0.1
                nextpos2 = listOfParticles[j].pos + listOfParticles[j].velocity*0.1 #assume dt=0.1
                if mag(nextpos2 - nextpos1) < distance: #if they collide with each other, transfer momentum
                    rhat = norm(diff) #unit vector of displacement
                    mv1 = listOfParticles[i].mass*listOfParticles[i].velocity #momentum of first particle
                    mv2 = listOfParticles[j].mass*listOfParticles[j].velocity #momentum of second particle
                    transfer = 2.*dot(listOfParticles[i].mass*mv2-listOfParticles[j].mass*mv1,rhat)/(listOfParticles[i].mass+listOfParticles[j].mass)*rhat #momentum transferred
                    listOfParticles[i].velocity = (mv1 + transfer)/listOfParticles[i].mass
                    listOfParticles[j].velocity = (mv2 - transfer)/listOfParticles[j].mass
 
#Define initial parameters: mass of system, inital temperature of system, initial energy of system, and length of container
m = 100 #mass (g)
T = 0 #Initial Temp (K)
Etotal = 0 #Inital total energy input
dE = 1000 #incremental energy change (J), how much energy is added to our system for each step of the program. You are advised NOT to change dE.
L_box = 6 # Define the length of our container
 
#Create our objects: container, sphere for solid phase, blue box for liquid phase, and empty list for gas particles
container = box(pos=vec(0,0,0), size=vec(L_box,L_box,L_box), color=color.white, opacity=0.1) # Creates a box of length L_box
solid = sphere(pos=vec(0,0,0), radius=L_box/2, color=color.white) #Creates a sphere for the solid phase
liquid = box(pos=vector(0,-L_box/2,0), size=vector(L_box,0,L_box), color=color.blue, opacity=0.75, visible=False) #Creates a box for the liquid phase
listOfParticles = [] #Creates an empty list of gas particles for the gas phase
 
#Define properties of our material: heat capacities, latent heats, and transition temperatures
c_s=2.108 #solid heat capacity (J/gK)
Hfus=335.5 #Latent heat of fusion (J/g)
c_l=4.186 #liquid heat capacity (J/gK)
Hvap=2260 #Latent heat of vaporization (J/g)
c_g=1.996 #gas heat capacity (J/gK)
Tm=273 #Melting point (K)
Tb=373 #Boiling point (K)
 
#Calculate total energy values at different points (J)
Esol=5e4 #Energy to raise temp to melting point, i.e. max energy a solid can have
Emelt=1e5 #Energy to raise temp AND melt all of the solid
Eliq=2e5 #Energy to raise temp, AND melt, AND reach boiling point, i.e. max energy a liquid can have
Eboil=4e5 #Energy melt AND reach boiling point AND boil all the liquid
 
#Initialize Graph
Grph1 = graph(title='Temperature vs Energy', xtitle='Energy Input to System (J)', ytitle='Temperature (K)', fast=False, ymin=0, ymax=1000) #initialize our graph axes, titles, and boundaries
HeatingCurve = gcurve(color=color.red, label='Heating Curve') #Prepare a data series to be plotted
 
Efinal = 1.25*Eboil #Set the final energy to stop the program at
while Etotal < Efinal: #Run loop until Energy is larger than Efinal
    rate(25) #Change this to make your program run faster or slower. 10-100 is recommended.
 
    if Etotal < Esol: #If statement for changing temp within solid phase
 
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    elif Etotal < Emelt: #If statement for changing from solid to liquid
        liquid.visible=True #make sure the liquid phase is visible
        ShrinkSolidGrowLiquid() #Change sizes of solid and liquid phases
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    elif Etotal < Eliq: #If statement for changing temp within liquid phase
        solid.visible=False #make sure the solid phase is invisible
 
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    elif Etotal < Eboil: #If statement for changing from liquid to gas
        ShrinkLiquid() #Change size of liquid phase
        MakeNewParticle() #Add a gas atom to the container
        ParticleMovementAndCollisions() #Make the gas particles move and collide
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    else: #Changing temperature within gas phase
        liquid.visible=False #make sure the liquid phase is invisible
 
        ParticleMovementAndCollisions() #Make the gas particles move and collide
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    Etotal = Etotal + dE # Increase the total energy by dE

If the particle movement is low, the matter is in the solid state.

1. The gas state is reached as particles exhibit very high energy at a correspondingly high temperature.
2. When a gas loses so much energy it turns into a liquid, it undergoes condensation.
3. Since particles in a solid are closely packed together, they can only move vibrationally .
4. Particles exhibit high velocities in the highest energy state.
5. Solid particles that absorb so much energy they turn into a gas undergo sublimation.
6. At moderate levels of kinetic energy, the particles can move freely and the matter exists as a liquid.
7. Lower energy means slower particle movement and lower temperature.
8. Theoretically, no particle movement occurs at -273.15 °C (0 K).
9. Solids typically have lower temperatures than gases.
10. If a gas is super heated to thousands of Kelvin, it ionizes and becomes plasma.
11. Increases in temperature result in greater particle velocity and therefore greater kinetic energy.
12. The Kinetic Theory of Matter says that for hotter temperatures, the more of the particles move in matter.

1. 
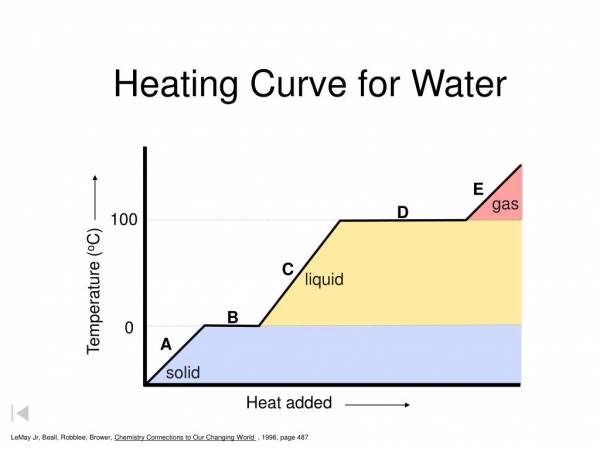
2. The first plateau is where the matter melts (goes from solid to liquid) or freezes (goes from liquid to solid). Likewise, the second plateau is where the matter boils/vaporizes (goes from liquid to gas) or condenses (goes from gas to liquid)
3. See graph and previous answer
4. 273.1 K (0 °C)
5. 373.1 K (100 °C)
6. The graph accurately models the changes between the solid, liquid, and gas phases of water, but does not include the process of ionization
7. The first plateau is longer than the second. This indicates that the heat capacity of liquid water is higher than the heat capacity of steam. This means that water is more efficient and carrying heat; it requires more energy to change its temperature in the liquid phase versus the gaseous phase

1. No. We know kinetic energy is equal to $\dfrac{1}{2}mv^2$. Rearranging for velocity, we find $v=\sqrt{\dfrac{2KE}{m}}$. Therefore, for the same energy level, more mass results in less velocity.
2. $Q=mc\Delta T$ and $Q=mL$
3. The mass, specific heat capacities, latent heat of fusion, latent heat of vaporization will not change. Energy input is an independent variable and temperature of the substance is a dependent variable.
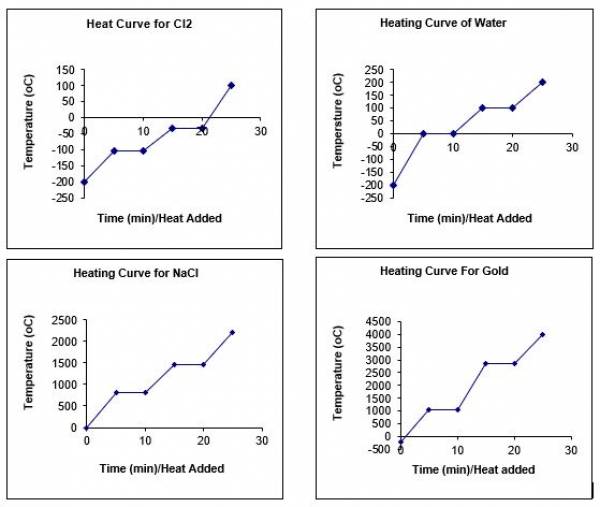
4. We can show different heating curves for different substances by changing the parameters defined in lines 56-62 (specific heat capacities, latent heat of fusion, melting point, etc.)
5. Here are some examples:
6. If the model occurred at 2 atmospheres of pressure, the melting/freezing point would lower and the boiling/condensing point would increase. We can look at a phase diagram to see how pressure affects change of state for different substances. One equation that relates pressure, temperature, and volume is the ideal gas law: $PV=nRT$ (note that this only applies to gases)

Link

GlowScript 2.7 VPython
#COLLAPSE LINES 3, 8, 11, AND 16! These are special bundles of code, called subroutines, which help simplify the coding later in the program.
def ShrinkSolidGrowLiquid():#This subroutine changes the sizes of the solid and liquid phases during melting
    solid.pos=solid.pos+vec(0,-(L_box/(2*ceil(m*Hfus/dE))),0) #SizeIncrement1=L_box/(2*ceil(m*Hfus/dE))
    solid.radius=solid.radius-(L_box/(2*ceil(m*Hfus/dE)))
    liquid.pos=liquid.pos+vec(0,0.5*(L_box/(2*ceil(m*Hfus/dE))),0)
    liquid.size=liquid.size+vec(0,(L_box/(2*ceil(m*Hfus/dE))),0)
def ShrinkLiquid():#This subroutine changes the size of the liquid phase during vaporization
    liquid.pos=liquid.pos+vec(0,-0.5*L_box/(2*ceil(m*Hvap/dE)),0) #SizeIncrement2=L_box/(2*ceil(m*Hvap/dE))
    liquid.size=liquid.size+vec(0,-L_box/(2*ceil(m*Hvap/dE)),0)
def MakeNewParticle():#This subroutine creates a new gas particle and adds it to a list of particles
    newparticle = sphere(pos=vector(L_box*(random()-0.5),(L_box-liquid.size.y)*(random()-0.5)+liquid.size.y/2,L_box*(random()-0.5)),radius=0.05, color=color.cyan)
    newparticle.mass = 1
    newparticle.velocity = vector(random()-0.5,random()-0.5,random()-0.5)*2 #the coefficient of 2 is a scaling factor for visual effect
    listOfParticles.append(newparticle)
def ParticleMovementAndCollisions(): #This subroutine moves gas particles and handles particle-wall and particle-particle collisions
    for particle in listOfParticles:
        if Etotal > Eboil: #If all the liquid has evaporated, start increasing the velocity of the gas particles
            particle.velocity=particle.velocity+sqrt(2*dE/particle.mass)*(particle.velocity/mag(particle.velocity))*2E-4 #Increase velocity with increasing energy. The coefficient of 2E-4 is a scaling factor for visual effect
        particle.pos = particle.pos + particle.velocity*0.1 #Update particle position, assume dt=0.1
        if abs(particle.pos.x) >= container.length/2:#Particle-wall collision in x
            particle.velocity.x = - particle.velocity.x
        if abs(particle.pos.y) >= container.height/2 or particle.pos.y <= (liquid.size.y-L_box/2):#Particle-wall collision in y
            particle.velocity.y = - particle.velocity.y
        if abs(particle.pos.z) >= container.width/2:#Particle-wall collision in z
            particle.velocity.z = - particle.velocity.z
    for i in range(0,len(listOfParticles)):#Particle-particle collisions, loop through every particle
        for j in range(i+1,len(listOfParticles)):#loop through every OTHER particle
            diff = listOfParticles[j].pos - listOfParticles[i].pos #displacement vector between two particles
            distance = mag(diff) #magnitude of displacement is distance
            if distance <= listOfParticles[i].radius + listOfParticles[j].radius: #if particles will collide, check their next positions
                nextpos1 = listOfParticles[i].pos + listOfParticles[i].velocity*0.1 #assume dt=0.1
                nextpos2 = listOfParticles[j].pos + listOfParticles[j].velocity*0.1 #assume dt=0.1
                if mag(nextpos2 - nextpos1) < distance: #if they collide with each other, transfer momentum
                    rhat = norm(diff) #unit vector of displacement
                    mv1 = listOfParticles[i].mass*listOfParticles[i].velocity #momentum of first particle
                    mv2 = listOfParticles[j].mass*listOfParticles[j].velocity #momentum of second particle
                    transfer = 2.*dot(listOfParticles[i].mass*mv2-listOfParticles[j].mass*mv1,rhat)/(listOfParticles[i].mass+listOfParticles[j].mass)*rhat #momentum transferred
                    listOfParticles[i].velocity = (mv1 + transfer)/listOfParticles[i].mass
                    listOfParticles[j].velocity = (mv2 - transfer)/listOfParticles[j].mass
 
#Define initial parameters: mass of system, inital temperature of system, initial energy of system, and length of container
m = 100 #mass (g)
T = 0 #Initial Temp (K)
Etotal = 0 #Inital total energy input
dE = 1000 #incremental energy change (J), how much energy is added to our system for each step of the program. You are advised NOT to change dE.
L_box = 6 # Define the length of our container
 
#Create our objects: container, sphere for solid phase, blue box for liquid phase, and empty list for gas particles
container = box(pos=vec(0,0,0), size=vec(L_box,L_box,L_box), color=color.white, opacity=0.1) # Creates a box of length L_box
solid = sphere(pos=vec(0,0,0), radius=L_box/2, color=color.white) #Creates a sphere for the solid phase
liquid = box(pos=vector(0,-L_box/2,0), size=vector(L_box,0,L_box), color=color.blue, opacity=0.75, visible=False) #Creates a box for the liquid phase
listOfParticles = [] #Creates an empty list of gas particles for the gas phase
 
#Define properties of our material: heat capacities, latent heats, and transition temperatures
c_s=2.108 #solid heat capacity (J/gK)
Hfus=335.5 #Latent heat of fusion (J/g)
c_l=4.186 #liquid heat capacity (J/gK)
Hvap=2260 #Latent heat of vaporization (J/g)
c_g=1.996 #gas heat capacity (J/gK)
Tm=273 #Melting point (K)
Tb=373 #Boiling point (K)
 
#Calculate total energy values at different points (J)
Esol=m*c_s*(Tm-T) #Energy to raise temp to melting point, i.e. max energy a solid can have
Emelt=Esol+m*Hfus #Energy to raise temp AND melt all of the solid
Eliq=Emelt+m*c_l*(Tb-Tm) #Energy to raise temp, AND melt, AND reach boiling point, i.e. max energy a liquid can have
Eboil=Eliq+m*Hvap #Energy to reach melting point, melt, reach boiling point, and boil all the liquid
 
#Initialize Graph
Grph1 = graph(title='Temperature vs Energy', xtitle='Energy Input to System (J)', ytitle='Temperature (K)', fast=False, ymin=0, ymax=1000) #initialize our graph axes, titles, and boundaries
HeatingCurve = gcurve(color=color.red, label='Heating Curve') #Prepare a data series to be plotted
 
Efinal = 1.25*Eboil #Set the final energy to stop the program at
while Etotal < Efinal: #Run loop until Energy is larger than Efinal
    rate(25) #Change this to make your program run faster or slower. 10-100 is recommended.
 
    if Etotal < Esol: #If statement for changing temp within solid phase
        T=T+dE/(m*c_s) #Calculate temperature (K) from q=mc(Delta_T) equation
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    elif Etotal < Emelt: #If statement for changing from solid to liquid
        liquid.visible=True #make sure the liquid phase is visible
        ShrinkSolidGrowLiquid() #Change sizes of solid and liquid phases
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    elif Etotal < Eliq: #If statement for changing temp within liquid phase
        solid.visible=False #make sure the solid phase is invisible
        T=T+dE/(m*c_l) #Calculate temperature (K) from q=mc(Delta_T) equation
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    elif Etotal < Eboil: #If statement for changing from liquid to gas
        ShrinkLiquid() #Change size of liquid phase
        MakeNewParticle() #Add a gas atom to the container
        ParticleMovementAndCollisions() #Make the gas particles move and collide
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    else: #Changing temperature within gas phase
        liquid.visible=False #make sure the liquid phase is invisible
        T=T+dE/(m*c_g) #Calculate temperature (K) from q=mc(Delta_T) equation
        ParticleMovementAndCollisions() #Make the gas particles move and collide
        HeatingCurve.plot(Etotal, T) #Plot T(K) vs E in J
 
    Etotal = Etotal + dE # Increase the total energy by dE