Triathlete's Dilemma
Activity Information
Learning Goals
- Analyze constant motion
- Use geometry/trigonometry to determine distance
- Analyze graphs
- Examine effect of changing variables in a problem situation
Prior Knowledge Required
- 2-D vectors
- Pythagorean Theorem
Code Manipulation
- Modify existing code
- Copy and paste code
- Create and use while loops
- Translate physical quantities and equations into code
—-
Activity
Handout
Triathlete's Dilemma

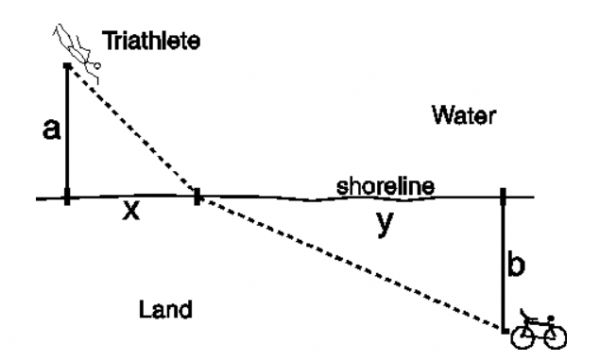
You are a triathlete in the water and you need to get to your bike parked in a rack at a specific location on the shore in the shortest amount of time possible. You can run faster than you can swim. Do you swim directly to the shore, then run to your bike? Do you swim to a point closer to your bike, then run? How do you solve this dilemma? Here are the specific parameters:
- The shoreline is linear and coincident with the x-axis
- You are in the water at the following coordinates, labeled “Start”: (-50,120)
- Your bike is parked at these coordinates, labelled “End: (100,-50)
- You are a well-conditioned athlete and can swim at 2 m/s and run at 9 m/s
Your goal is to determine the optimal x-coordinate shore point to swim towards to get to your bike in the shortest possible time. Using the starter code below, decide what you need in order to compute the sim time and corresponding run time. You are probably aware that there is no reason to swim away from your bike or beyond your bike, so limit your shore point analysis to the x-axis range established by the initial x-coordinates of the Start and End locations. As a starting point, you should consider every half meter point along the shoreline.
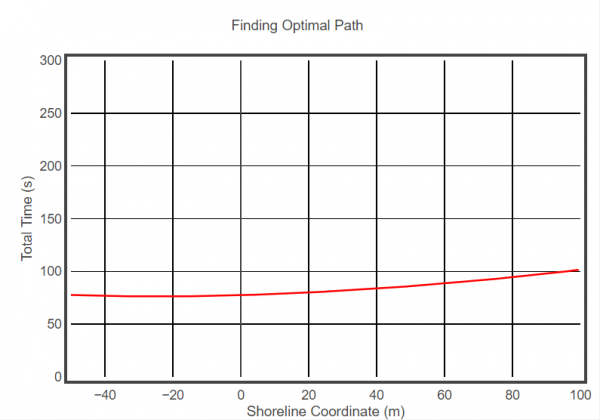
You will examine your total time results graphically. Notice in the code, that the graph commands are already there, but the graph won't be generated until you produce some data. Your “while” loop should include a calculation for the swim time, run time, and total time for each half-meter position along the beach. Your graph will plot corresponding shore positions versus total time.
Extension questions:
- How could you modify your code to get greater precision in your answer? What specific changes would you make?
- What happens to the critical shore point if you swim faster?
- What happens if you change this situation? Suppose it's a sea lion in the water trying to get to the bike! Reverse your original speeds—Make the swim speed 9 m/s and the run speed 2 m/s. What is the new shore point for the fastest travel time now?
- Use the accompanying picture below to help answer this question. The distance from the shoreline to the swimmer (a) is 65 m. The distance from the shoreline to the bike (b) is 83 m. The sum of (x) and (y) is 135 m. The person can swim at 1.56 m/s and can run at 8.75 m/s. Solve for (x) to produce the shortest time possible to get your starting point in the water to your bike.
Code
Answer Key
Handout
Our first modifications to the code are defining the variables “target” (line 22), and “final” (line 24). This represents at which x-coordinate you reach the shore and the x-coordinate of the bike rack, respectively. We add the variable “dt” (line 23) which is a miniscule increment in time, and used later in our while loop. We then create equations for the “swimtime” and “runtime” variables (lines 25 & 26); these equations are just a rearranged form of the Pythagorean Theorem solved for the length of the hypotenuse and divided by the swim speed and run speed variables—remember that distance divided by speed is time. Finally, the limits of the while loop are defined (line 35) and the swim time and run time equations are reentered (lines 37 & 38). Looking at the output graph, the optimal x-coordinate along the shore line is equal to -24.5.
Extension Solutions:
- In order to increase the precision of your answer, you can decrease the size of the “dt” variable. The smaller this variable, the more points along the graph the program will plot, and thus the more precise you can be with your answer. An exact answer, however, requires calculus to solve.
- The faster the swim speed, the further in the positive x-direction your critical shore point will be
- For the theoretical sea lion situation where the speeds are flipped, the new shore point is the x-coordinate equal to 91.0, with a total travel time of 45.97 seconds. You can find this by simply modifying lines 18 and 19.
- To solve this question graphically, you simply have to modify the “start” and “end” variables (lines 12 & 13) to match the new distances provided in the problem statement. As well, you have to adjust the “swimv” and “runv” variables to the new given speeds. Depending on how small you make your “dt” variable, the optimal shore critical point (x) approaches 9.77 meters.
Code