There are times when you will observe systems that have move around some central axis in a very regular fashion. For example, the Moon revolves around the Earth in an orbit that is nearly circular. In doing so, it moves with nearly the same speed (not velocity!) at every location in its orbit. A system whose motion can be modeled as moving in a circular orbit at constant speed is said to execute “uniform circular motion.” It is called “uniform” because the speed of the system doesn't change. The velocity is always changing direction, but not size. In these notes, you read about a special mathematical form that the net force takes when the motion of the system is uniform and circular.

The Moon orbiting the Earth with a speed $v$ and at a distance $R$ from the Earth.

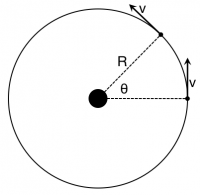
Consider that the moon orbits the Earth with a constant speed. The figure to the right shows the set up. The Moon orbits the Earth with a constant speed, $v$, at a distance $R$ from the Earth. In a time $\Delta t$, the Moon has moved from one location (on the x-axis) to another location. It has moved an angular distance of $\theta$.

For this situation, we know the only force exerted on the Moon is gravitational force due to the Earth. Hence, the gravitational force is the net force. Using the momentum principle, you will find that the net force takes a special form in the case on uniform circular motion. Let's write down the momentum principle,

$$ \vec{F}_{net} = \dfrac{\Delta \vec{p}}{\Delta t} = m \dfrac{\Delta \vec{v}}{\Delta t} $$

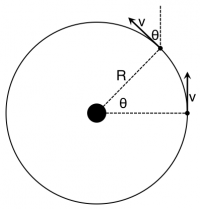
Because the mass of the Moon remains unchanged, we will only need to determine how the velocity is changing ¹⁾. You can determine the vector components for both the final and initial velocities in the picture to the right. In the picture to the below, the angle $\theta$ that the final velocity makes with the vertical has been labeled ²⁾

The final vector velocity can be decomposed along the x and y directions once you know which angle is \theta.

From this representation, we can find the components for the initial and final velocity vectors and apply the momentum principle to them.

$$ \vec{F}_{net} = \dfrac{\Delta \vec{p}}{\Delta t} = m \dfrac{\Delta \vec{v}}{\Delta t} $$

$$ \vec{F}_{net} = m \dfrac{\langle -v \sin \theta, v \cos \theta\rangle - \langle 0, v \rangle}{\Delta t} $$

$$ \vec{F}_{net} = m \dfrac{\langle -v \sin \theta, v \cos \theta - v \rangle}{\Delta t} = mv \dfrac{\langle - \sin \theta, \cos \theta - 1 \rangle}{\Delta t}$$

$$ \Delta t = \dfrac{R\theta}{v} $$

$$ \vec{F}_{net} = \dfrac{mv^2}{R\theta} \langle - \sin \theta, \cos \theta - 1 \rangle $$

\begin{eqnarray*} \sin \theta \approx \theta\\ \cos \theta \approx 1 \end{eqnarray*}

$$ \vec{F}_{net} = \dfrac{mv^2}{R\theta} \langle - \theta, 0 \rangle $$

$$ \vec{F}_{net} = \langle - \dfrac{mv^2}{R}, 0 \rangle $$