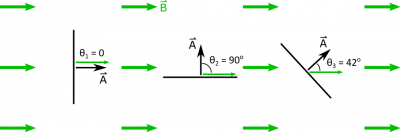
Suppose you have a magnetic field $\vec{B} = 0.6 \text{ mT } \hat{x}$. Three identical square loops with side lengths $L = 0.5 \text{ m}$ are situated as shown below. The perspective shows a side view of the square loops, so they appear very thin even though they are squares when viewed face on.

• The orientations of the square loops are as indicated above. They can be described by their angles with respect to the magnetic field. $\theta_1 = 0$, $\theta_2 = 90^\text{o}$, $\theta_3 = 42^\text{o}$.
• The magnetic field is $\vec{B} = 0.6 \text{ mT } \hat{x}$.
• The length of a square's side is $L = 0.5 \text{ m}$.

• The magnetic flux through each loop.

• The loops have flat faces.
• The magnetic field does not change with time, and is uniform in space.

• We represent magnetic flux through an area as

$$\Phi_B = \int \vec{B} \bullet \text{d}\vec{A}$$

• We represent the situation with the given representation in the example statement above.

Since the magnetic field has a uniform direction, and the area of the loop is flat (meaning $\text{d}\vec{A}$ does not change direction either), then we can simplify the dot product: $$\vec{B} \bullet \text{d}\vec{A} = B\text{d}A\cos\theta$$

Since $B$ and $\theta$ do not change for different little pieces ($\text{d}A$) of the area, we can pull them outside the integral:

$$\int B\text{d}A\cos\theta =B\cos\theta \int \text{d}A = BA\cos\theta$$

Area for a square is just $A = L^2$, and $\theta$ is different for each loop:

\[ \Phi_B = \begin{cases} BL^2\cos 0 = 1.5 \cdot 10^{-4} \text{ Tm}^2 & \text{Loop 1} \\ BL^2\cos 90^\text{o} = 0 \text{ Tm}^2 & \text{Loop 2} \\ BL^2\cos 42^\text{o} = 1.1 \cdot 10^{-4} \text{ Tm}^2 & \text{Loop 3} \end{cases} \]

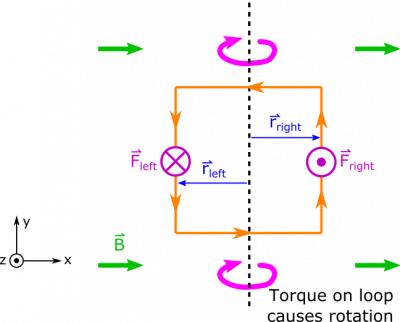
It remains to find the direction of the force, for which we will use the Right Hand Rule. You should be able to convince yourself based on the coordinates we have chosen that the force on the left side is in the $+\hat{z}$ direction, and the force on the right side is in the $-\hat{z}$ direction.

This means that the net force on the loop is $0$, the loop's center of mass won't move! However, the opposing forces on opposite sides will cause the loop to spin – there is a torque! The calculation for the torque is shown below, with a diagram included to show visually what happens.

The calculation is here:

$$\vec{\tau} = \vec{r} \times \vec{F} = \vec{r}_\text{left} \times \vec{F}_\text{left} + \vec{r}_\text{right} \times \vec{F}_\text{right} = \left(-\frac{L}{2} \hat{x}\right) \times \left(IBL \hat{z}\right) + \left(\frac{L}{2} \hat{x}\right) \times \left(-IBL \hat{z}\right) = IBL^2 \hat{y}$$