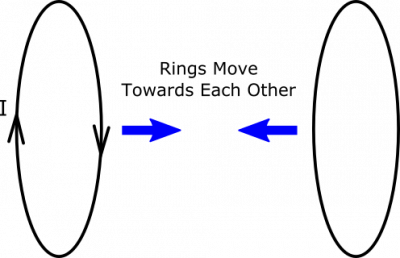
Suppose you have two conducting rings centered on the same axis so that they face one another. One of the rings has a current in it, which produces a magnetic field nearby. The rings are moved towards one another. What happens?

• The rings are oriented so that there is a magnetic flux through one due to to the other.

• A description of the magnetic flux and/or induced current.

• There is no current in the second ring before the rings are moved.
• There is no power source for the first ring's current, and so it is free to change in response to changing magnetic fields.

• We represent magnetic flux through an area as

$$\Phi_B = \int \vec{B} \bullet \text{d}\vec{A}$$

• We represent the steps with the following visual:

Since the magnetic field has a uniform direction, and the area of the loop is flat (meaning $\text{d}\vec{A}$ does not change direction if we move along the area), then we can simplify the dot product: $$\int \vec{B} \bullet \text{d}\vec{A} = \int B\text{d}A\cos\theta$$

Since $B$ and $\theta$ do not change for different little pieces ($\text{d}A$) of the area, we can pull them outside the integral:

$$\int B\text{d}A\cos\theta =B\cos\theta \int \text{d}A = BA\cos\theta$$

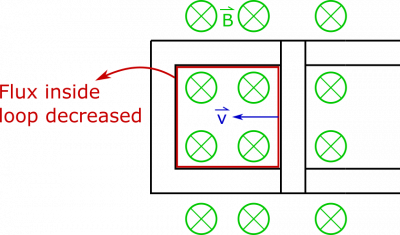
It will be easier to concern ourselves with this value, rather than try to describe the integral calculation each time. The bar begins moving to the left and the area begins to close up, as shown below:

It should be easy to see the that the magnetic field and the orientation of the loop are not changing, but the area of the loop is decreasing. The flux through the loop is therefore decreasing, which indicates that a current is induced in the loop.

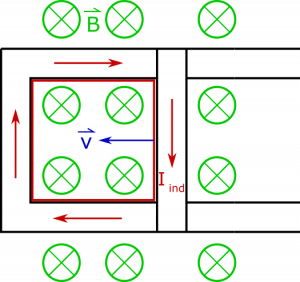
To determine the direction of the current, consider that when we say the flux decreases, this carries the assumption that the area vector points in the same direction as the magnetic field, which is into the page. The induced current should create a magnetic field that opposes the change in flux. The change in flux is a “decrease”, so we expect the induced current to create a “positive” magnetic field, just meaning that it is pointing in the same direction as the area-vector. Since the area vector points into the page, we expect for the induced current to be clockwise. We determine this using the Right Hand Rule.

Alternatively, you could think of the mobile charges inside the moving bar. Since the bar is moving inside a magnetic field, mobile charges will experience an acceleration due to the magnetic force. The force is $\vec{F} = q \vec{v} \times \vec{B}$, which points down for positive charges, implying that conventional current will be clockwise, which is the same result we reached earlier. The result is shown below.