Suppose you are given the following graph of current over time. You can see that the first peak is at the point where $t=0.01\text{ s}$, and $I=0.3\text{ A}$. The graph is shown below. Find the amplitude, period, and frequency of the current, and give an equation that describes the alternating current.

• The first peak in the graph is at $(t=0.01\text{ s}, I=0.3\text{ A})$.

• Amplitude, period, frequency.
• Equation for alternating current.

• The graph of the current is a sine wave.
• As indicated on the graph, at $t=0$, we have $I=0$.
• The current is centered about $I=0$, that is, the sine wave has not been shifted vertically at all.

• We represent the graph as given in the example statement.

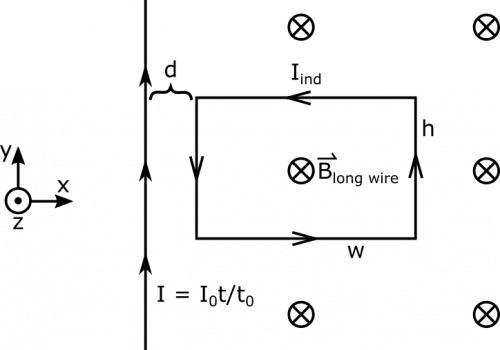
In order to find the induced voltage, we will need the magnetic flux. This requires defining an area-vector and determining the magnetic field. We can use the right hand rule to determine the the magnetic field from the wire is into the page ($-\hat{z}$) near the rectangle. For convenience, we will also define for the area vector to be into the page. Since they both point in the same direction, the dot product simplifies:

$$\Phi_B = \int \vec{B} \bullet \text{d}\vec{A} = \int B\text{d}A$$

Usually, we would pull the $B$ out of the integral, but we cannot do that in this case! That is because $B$ varies for different points in the rectangle's area. In order to see this a little more clearly, we will break the integral down a little and also insert the expression for the magnetic field from a long wire:

$$\int_{\text{rectangle}} B\text{d}A = \int_{\text{left to right}} \int_{\text{top to bottom}} B\text{d}x\text{d}y = \int_{x=d}^{x=d+w} \int_{y=0}^{y=h} \frac{\mu_0 I}{2 \pi x}\text{d}x\text{d}y$$

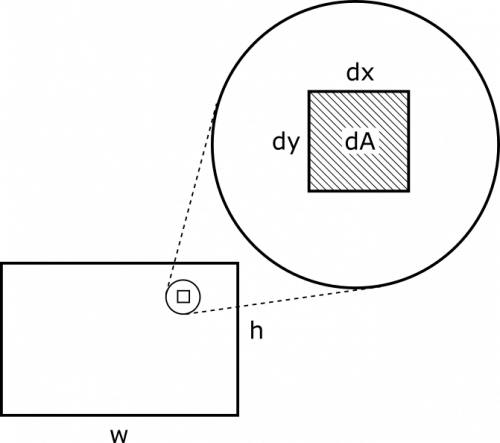
In the first equality, we just changed the integral from over the “rectangle” to be over its two dimensions, “left to right”, and “top to bottom”. We also changed $\text{d}A$ to be in terms of its two dimensions, $\text{d}A = \text{d}x\text{d}y$. A visual is shown below for clarity.

At this point, our integral is set up enough that we can crunch through the analysis. We can pull out constants to the front and calculate to the end:

\begin{align*} \int_{x=d}^{x=d+w} \int_{y=0}^{y=h} \frac{\mu_0 I}{2 \pi x}\text{d}x\text{d}y &= \frac{\mu_0 I}{2 \pi} \int_{d}^{d+w} \frac{\text{d}x}{x} \int_{0}^{y} \text{d}y \\ &= \frac{\mu_0 I}{2 \pi} \left[\log x \right]_{d}^{d+w} \left[ y \right]_{0}^{y} \\ &= \frac{\mu_0 I}{2 \pi} \left(\log(d+w) - \log(d)\right) \left( h-0 \right) \\ &= \frac{\mu_0 I h}{2 \pi} \log\left(\frac{d+w}{d}\right) \end{align*}

At this point, we are equipped to find the induced voltage. Notice that everything in the magnetic flux expression is constant in time, except for to current, $I$. Here is the induced voltage:

$$V_{ind} = -\frac{\text{d}\Phi}{\text{d}t} = -\frac{\mu_0 h}{2 \pi} \log\left(\frac{d+w}{d}\right)\frac{\text{d}I}{\text{d}t} = -\frac{\mu_0 h}{2 \pi} \log\left(\frac{d+w}{d}\right)\frac{I_0}{t_0}$$

Notice that the induced voltage is negative. This means that the induced current produces a magnetic fields whose corresponding flux is negative flux. Since the area-vector was defined as into the page ($-\hat{z}$), this means that the magnetic field produced by the induced current should be out of the page ($+\hat{z}$). By the right hand rule, this means the induced currents is directed counterclockwise. See below for a visual.