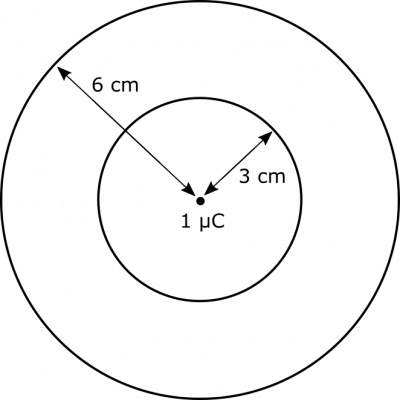
Suppose you have a point charge with value $1 \mu\text{C}$. What are the fluxes through two spherical shells centered at the point charge, one with radius $3 \text{ cm}$ and the other with radius $6 \text{ cm}$?

• The point charge has charge $q=1 \mu\text{C}$.
• The two spheres have radii $3 \text{ cm}$ and $6 \text{ cm}$.

• $\Phi_e$ for each sphere
• $\text{d}\vec{A}$ or $\vec{A}$, if necessary

• There are no other charges that contribute appreciably to the flux calculation.
• There is no background electric field.
• The electric flux through the spherical shells are due only to the point charge.

• We represent the electric flux through a surface with:

$$\Phi_e=\int\vec{E}\bullet \text{d}\vec{A}$$

• We represent the electric field due to a point charge with:

$$\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r}$$

• We represent the situation with the following diagram. Note that the circles are indeed spherical shells, not rings as they appear.

Before we dive into calculations, let's consider how we can simplify the problem. Think about the nature of the electric field due to a point charge, and of the $\text{d}\vec{A}$ vector for a spherical shell. The magnitude of the electric field will be constant along the surface of a given sphere, since the surface is a constant distance away from the point charge. Further, $\vec{E}$ will always be parallel to $\text{d}\vec{A}$ on these spherical shells, since both point directly away from the point charge. A more in depth discussion of these symmetries can be found in the notes of using symmetry to simplify our flux calculation.

Since $\vec{E}$ is constant with respect to $\text{d}\vec{A}$ (in this case, it is sufficient that $\vec{E}$ is parallel to $\text{d}\vec{A}$ and has constant magnitude), we can rewrite our flux representation:

$$\Phi_e=\int\vec{E}\bullet \text{d}\vec{A} = \left|\vec{E}\right|\int\text{d}\left|\vec{A}\right|$$

We can rewrite $\left|\vec{E}\right|$ since it is constant on the surface of a given spherical shell. We use the formula for the electric field from a point charge.

$$\left|\vec{E}\right| = \frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2}\left|\hat{r}\right| = \frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2}$$

We can plug in values for $q$ and $r$ for each spherical shell, using what we listed in the facts. For the smaller shell, we have $\left|\vec{E}\right|=1.0\cdot 10^7 \text{N/C}$. For the larger shell, we have $\left|\vec{E}\right|=2.5\cdot 10^6 \text{N/C}$.

To figure out the area integral, notice that the magnitude of the area-vector is just the area. This means that our integrand is the area occupied by $\text{d}A$. Since we are integrating this little piece over the entire shell, we end up with the area of the shell's surface: $$\int\text{d}\left|\vec{A}\right|=\int\text{d}\vec{A}=A$$

In order to find electric flux, we must first find $\vec{A}$. Remember in the notes on flux that area can be a vector when we define it as a cross product of width and length vectors. Here, we can use the following for width and length, with width being the top of the rectangle, and pointing out of the page, and length being the longer side, and pointing at an upwards angle: $$\vec{w}=3\text{ m }\hat{z}$$ $$\vec{l}=5\text{ m }\cdot\cos 30^\circ (\hat{x})+5\text{ m }\sin 30^\circ\hat{y} = 2.5\sqrt{3}\text{ m } \hat{x} + 2.5\text{ m }\hat{y}$$ Now, we can find the area vector: \begin{align*} \vec{A} &= \vec{l}\times\vec{w} \\ &= (2.5\sqrt{3}\text{ m } \hat{x} + 2.5\text{ m }\hat{y}) \times (3\text{ m }\hat{z}) \\ &= 7.5\sqrt{3}\text{ m}^2 (-\hat{y}) + 7.5\text{ m}^2\hat{x} \\ &= 7.5\text{ m}^2\hat{x} - 7.5\sqrt{3}\text{ m}^2 \hat{y} \end{align*} Again, since the rectangle is not a closed surface, the choice for direction of $\vec{A}$ was arbitrary, and it would have been just fine to define it oppositely. Anyways, we can proceed to determine the electric flux: \begin{align*} \Phi_e &= \vec{E}\bullet\vec{A} \\ &= (8\text{ V/m } \hat{x}) \bullet (7.5\text{ m}^2\hat{x} - 7.5\sqrt{3}\text{ m}^2 \hat{y}) \\ &= 60\text{ Vm} \end{align*}