Section 6.3 in Matter and Interactions (4th edition)
Work Done by Non-Constant Forces
Until now, the definition of work that has been used is for forces that are constant vectors (constant in magnitude and direction). In these notes, you will read about how to determine the work done by forces that change (either in their magnitude or direction).
Lecture Video
Work done in small steps
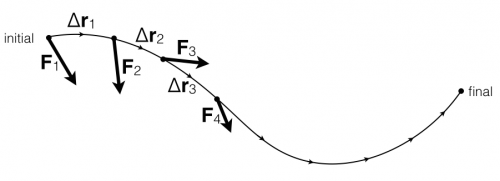
Consider a particle that is moving along a curved path where the force changes at every instant in some way. The particle moves from an initial location to a final location, and you want to calculate the work acting on that particle over the entire path.
You could do this cutting up the path into little chunks and determining the work done in each chunk. The average force on the particle at that point in the path is $\vec{F}_{1}$. Over that small interval the work done in the first chunk is,
$$W_{1} = \vec{F}_{1}\cdot\Delta \vec{r}_{1}$$
Each chunk would contribute a small amount, so that the total work could be estimated by,
$$W_{total} = W_{1} + W_{2} + W_{3} + \dots = \vec{F}_{1}\cdot\Delta \vec{r}_{1} + \vec{F}_{2}\cdot\Delta \vec{r}_{2} + \vec{F}_{3}\cdot\Delta \vec{r}_{3} + \dots = \sum_{i=l}^N \vec{F}_i\cdot\Delta\vec{r}_i$$
General Definition of Work done by a Force
If we make each chunk smaller (and thus have more chunks), the estimate would get better. In the limit that the chunks become infinitesimally small, the sum becomes an integral along the path.
$$W_{total} = \int_i^f \vec{F}\cdot d\vec{r}$$
This is the general definition of the work done by a force. It is true even if the force isn't constant and if the path is curved. In this class, you will usually use it in only one-dimension,
$$W_{total} = \int_{x_i}^{x_f} F_x dx$$
Don't get hung up on the choice of the $x$-direction here, it's just meant to communicate that the integral is calculated along a single dimension because the object increases its velocity component in only one direction.