Section 22.2 in Matter and Interactions (4th edition)
Changing Magnetic Flux
In these notes, we will start thinking the right hand side of Faraday's Law (the dΦBdt part) and what it means to have a changing magnetic flux. Let's start by defining what flux is.
In general, any sort of flux is how much of something goes through an area. For example, we could think of a child's bubble wand in terms of the air flux (from you blowing) through the circle (with the bubble solution in it). If you wanted to make bigger bubbles or make many more bubbles, you could do two things: increase the air flow or get a bubble wand with a bigger circle. Both of these actions (increasing the area and increasing the amount of air) will result in a larger “air flux” through the bubble wand. It's probably worth mentioning that we have assumed that you are holding the bubble wand so the circle is perpendicular to the air flow. If instead you rotate the wand 90 degrees, you will not get any bubbles since there is no air that is actually going through the circle part of the bubble wand. So the air flux not only depends on the amount of air and the area of circle, but also on how those two are oriented relative to each other. The idea of flux can be useful in many different contexts (i.e. fluids, electricity, air, etc.), but for any kind of flux, these are still the three conditions that matter: (1) the strength/amount, (2) the area, and (3) the orientation.
Therefore magnetic flux is the strength of the magnetic field on a surface area or rather the amount of the magnetic field that goes through an area. For magnetic flux, we need to consider: the strength of the magnetic field, the area that the field goes through, and the orientation of the magnetic field relative to the area. These notes will introduce the mathematics behind magnetic flux, which we will use in Faraday's Law.
Magnetic Flux
Just like we did before with electric flux, we will say that magnetic flux is the strength of the magnetic field over an area or rather the amount of magnetic field that goes through an area. How the magnetic field is oriented relative to the area does matter so we will again want to treat the area as vector. This is very similar to how we defined the electric flux before. Mathematically, we represent the magnetic flux as:
ΦB=→B∙→A
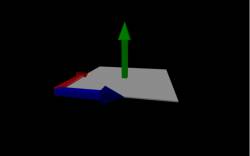
where ΦB is the magnetic flux (with units of T⋅m2), →B is the magnetic field and →A is the area vector. The area vector in this case is the vector that has the same magnitude as the area (i.e. length times width for a rectangular area or πr2 for a circular area) and has a direction that is perpendicular to the area, which is represented by the green arrow in the figure to the right. (This is exactly the same as with electric flux). You may notice that there are actually two different vectors that are perpendicular to the gray surface. We've drawn the green arrow in the +y direction, but we could have also picked the vector that points in the −y direction. For an open surface, it doesn't matter which of the perpendicular vectors you pick, as long as you are consistent after you pick one.
The dot product between the →B and the →A then tells you about the direction the magnetic field points relative to the area. Mathematically, we can simplify the dot product by saying: ΦB=|→B||→A|cos(θ)
(As a side note, this technically gives you the magnitude of the flux. Flux can be positive or negative and that depends on how the area vector points relative to the magnetic field vectors. This is discussed further in the page of notes on directions.)
In writing the magnetic flux above, we have made an assumption that the area vector points in the same direction everywhere on the surface (or rather that the area we are considering is flat rather than curved). If instead the surface is curved we would need to write the magnetic flux in terms of a very small area and then add the flux through each of those small areas together. Mathematically, we would do this with an integral: ΦB=∫→B∙d→A
Changing Magnetic Flux
As you saw in the demo video, just having a magnetic flux is not enough though - to drive a current, the magnetic flux must be changing. Mathematically, we write this change as a change in the magnetic flux over a change in time. Namely:
dΦBdt
If we assume that the change is happening at a constant rate, we can write this in terms of large changes (using deltas) - ΔΦBΔt. In this case, we only care about the initial and final flux relative to the initial and final time: ΔΦBΔt=ΦBf−ΦBitf−ti
If the change in flux is not happening at a constant rate, we then have to consider the instantaneous change in flux using the differential form: dΦBdt.
There are many ways that the magnetic flux could be changing - the size of the magnetic field could be increasing/decreasing, the size of the area could be getting bigger/smaller, the angle between the magnetic field and the area could be changing, or even some combination of these factors. The examples below go through a couple of these cases to show how you could calculate the change in the magnetic flux.