Magnetic Force on Moving Charge
Suppose you have a moving charge ($q=1.5 \text{ mC}$) in a magnetic field ($\vec{B} = 0.4 \text{ mT } \hat{y}$). The charge has a speed of $10 \text{ m/s}$. What is the magnetic force on the charge if its motion is in the $+x$-direction? The $-y$-direction?
Facts
- The charge is $q=1.5 \text{ mC}$.
- There is an external magnetic field $\vec{B} = 0.4 \text{ mT } \hat{y}$.
- The velocity of the charge is $\vec{v} = 10 \text{ m/s } \hat{x}$ or $\vec{v} = -10 \text{ m/s } \hat{y}$.
Lacking
- $\vec{F}_B$
Approximations & Assumptions
- The magnetic force on the charge contains no unknown contributions.
- The charge is moving at a constant speed (no other forces acting on it)
Representations
- We represent the magnetic force on a moving charge as
$$\vec{F}= q \vec{v} \times \vec{B}$$
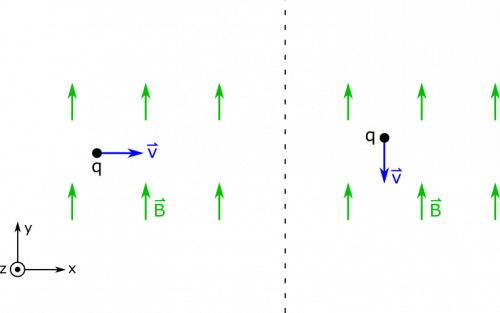
- We represent the two situations below.
Solution
Let's start with the first case, when $\vec{v}=10 \text{ m/s } \hat{x}$.
The trickiest part of finding magnetic force is the cross-product. You may remember from the math review that there are a couple ways to do the cross product. Below, we show how to use vector components, for which it's helpful to rewrite $\vec{v}$ and $\vec{B}$ with their components.
\begin{align*} \vec{v} &= \langle 10, 0, 0 \rangle \text{ m/s} \\ \vec{B} &= \langle 0, 4\cdot 10^{-4}, 0 \rangle \text{ T} \\ \vec{v} \times \vec{B} &= \langle v_y B_z - v_z B_y, v_z B_x - v_x B_z, v_x B_y - v_y B_x \rangle \\ &= \langle 0, 0, 4\cdot 10^{-3} \rangle \text{ T} \cdot \text{m/s} \end{align*}
Alternatively, we could use the whole vectors and the angle between them. We find that we obtain the same result for the cross product. One would need to use the Right Hand Rule to find that the direction of the cross product is $+\hat{z}$. The magnitude is given by
$$\left|\vec{v} \times \vec{B} \right|= \left|\vec{v}\right| \left|\vec{B} \right| \sin\theta = (10 \text{ m/s})(4\cdot 10^{-4} \text{ T}) \sin 90^{\text{o}} = 4\cdot 10^{-3} \text{ T} \cdot \text{m/s}$$
We get the same answer with both methods. Now, for the force calculation:
$$\vec{F}_B = q \vec{v} \times \vec{B} = 1.5 \text{ mC } \cdot 4\cdot 10^{-3} \text{ T} \cdot \text{m/s } \hat{z} = 6 \mu\text{N}$$
Notice that the $\sin 90^{\text{o}}$ is equal to $1$. This means that this is the maximum force that the charge can feel, and we get this value because the velocity and the B-field are exactly perpendicular. Any other orientation would have yielded a weaker magnetic force. In fact, in the second case, when the velocity is parallel to the magnetic field, the cross product evaluates to $0$. See below for the calculations.
\begin{align*} \vec{v} &= \langle 0, -10, 0 \rangle \text{ m/s} \\ \vec{B} &= \langle 0, 4\cdot 10^{-4}, 0 \rangle \text{ T} \\ \vec{v} \times \vec{B} &= \langle v_y B_z - v_z B_y, v_z B_x - v_x B_z, v_x B_y - v_y B_x \rangle \\ &= \langle 0, 0, 0 \rangle \end{align*}
Or, with whole vectors:
$$\left|\vec{v} \times \vec{B} \right|= \left|\vec{v}\right| \left|\vec{B} \right| \sin\theta = (10 \text{ m/s})(4\cdot 10^{-4} \text{ T}) \sin 0 = 0$$
When the velocity is parallel to the magnetic field, $\vec{F}_B=0$.