Example: Two Segments of Charge
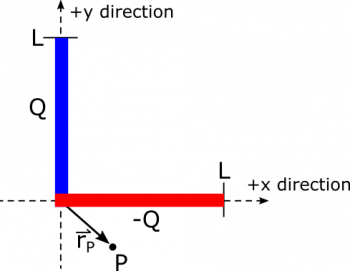
Suppose we have two segments of uniformly distributed charge, one with total charge $+Q$, the other with $-Q$. The two segments each have length $L$, and lie crossed at their endpoints in the $xy$-plane. The segment with charge $+Q$ lies along the $y$-axis, and the segment with charge $-Q$ lies along the $x$-axis. See below for a diagram of the situation. Create an expression for the electric field $\vec{E}_P$ at a point $P$ that is located at $\vec{r}_P=r_x\hat{x}+r_y\hat{y}$. You don't have to evaluate integrals in the expression.
Facts
- One segment lies on the $y$-axis stretching from $0$ to $L$, with charge $Q$ uniformly distributed.
- The other segment lies on the $x$-axis stretching from $0$ to $L$, with charge $-Q$ uniformly distributed.
- The point $P$ is at the arbitrary location $\vec{r}_P=r_x\hat{x}+r_y\hat{y}$
- The electric field due to a point charge is $$\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{r^3}\vec{r}$$
- The electric field at $P$ is the superposition of contributions from the two segments: $$\vec{E}_P = \vec{E}_{+Q} +\vec{E}_{-Q}$$
Goal
- Find $\vec{E}_P$.
Representations
Solution
Approximation
We begin with an approximation, which will make our calculations simpler, and makes sense based on our representation:
- The thicknesses of both segments are infinitesimally small, and we can approximate them as line segments.
This example is complicated enough that it's worthwhile to make a plan.
Plan
We will use integration to find the electric field from each segment, and then add the electric fields together using superposition. We'll go through the following steps.
- For the first segment, find the linear charge density, $\lambda$.
- Use $\lambda$ to write an expression for $\text{d}Q$.
- Assign a variable location to the $\text{d}Q$ piece, and then use that location to find the separation vector, $\vec{r}$.
- Write an expression for $\text{d}\vec{E}$.
- Figure out the bounds of the integral, and integrate to find electric field at $P$.
- Repeat the above steps for the other segment of charge.
- Add the two fields together to find the total electric field at $P$.
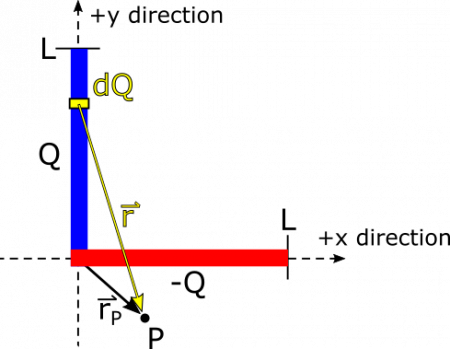
Because we know that electric fields add through superposition, we can treat each of the charges separately, find the electric field, then add the fields together at $P$ at the end. We can begin with the electric field due to the segment along the $y$-axis. We start by finding $\text{d}Q$ and $\vec{r}$. The charge is uniformly distributed so we have a simple line charge density of $\lambda=Q/L$. The segment extends in the $y$-direction, so we have $\text{d}l=\text{d}y$. This gives us $\text{d}Q$: $$\text{d}Q=\lambda\text{d}l=\frac{Q\text{d}y}{L}$$
Assumption
The charge is evenly distributed along each segment of charge. This allows each little piece of charge to have the same value along each line.
The separation vector $\vec{r}$ points from the source of the electric field to the observation point. The source is $\text{d}Q$, which is located at $y\hat{y}$, and the observation point is $\vec{r}_P=r_x\hat{x}+r_y\hat{y}$. Then we have the separation vector: $$\vec{r}=\vec{r}_P-y\hat{y}=r_x\hat{x}+r_y\hat{y}-y\hat{y}=r_x\hat{x}+(r_y-y)\hat{y}$$
Now, we have enough to define the electric field from the small piece ($\text{d}Q$) of the segment - plugging the $\text{d}Q$ and $\vec{r}$ we just found: $$\text{d}\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{\text{d}Q}{r^3}\vec{r}=\frac{1}{4\pi\epsilon_0}\frac{Q\text{d}y}{L\cdot|r_x\hat{x}+(r_y-y)\hat{y}|^3}(r_x\hat{x}+(r_y-y)\hat{y})$$
Next, we integrate over the entire segment to find an expression for its contribution to the electric field vector at $P$. The limits of our integral are based on the variable of integration, which is $y$. This denotes the length along the segment on the $y$-axis, which stretches from $0$ to $L$, so these are our limits of integration. $$\vec{E}_{+Q}=\int_0^L\frac{1}{4\pi\epsilon_0}\frac{Q\text{d}y}{L\cdot|r_x\hat{x}+(r_y-y)\hat{y}|^3}(r_x\hat{x}+(r_y-y)\hat{y})$$
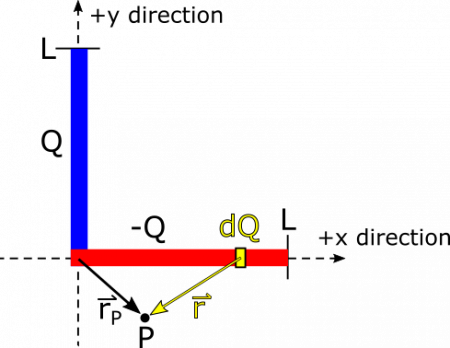
Next, we can do a similar analysis to find the electric field vector contribution from the segment that lies along the $x$-axis. See below for a visual of $\text{d}Q$ and $\vec{r}$. See if you can convince yourself that for the segment along the $x$-axis, $\text{d}Q=\frac{-Q\text{d}x}{L}$, and $\vec{r}=(r_x-x)\hat{x}+r_y\hat{y}$.
From here, we can find $\text{d}\vec{E}$: $$\text{d}\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{\text{d}Q}{r^3}\vec{r}=\frac{1}{4\pi\epsilon_0}\frac{-Q\text{d}x}{L\cdot|(r_x-x)\hat{x}+r_y\hat{y}|^3}((r_x-x)\hat{x}+r_y\hat{y})$$
To find the contribution from the entire segment, we again must determine the endpoints of our integration. Our variable of integration is $x$ this time, which denotes the distance along the segment that lies on the $x$-axis. This distance stretches from $0$ to $L$, so these are our limits of integration: $$\vec{E}_{-Q}=\int_0^L\frac{1}{4\pi\epsilon_0}\frac{-Q\text{d}x}{L\cdot|(r_x-x)\hat{x}+r_y\hat{y}|^3}((r_x-x)\hat{x}+r_y\hat{y})$$
Then the final electric field vector at $P$ is the sum of the two contributions, because of vector superposition. (You can pull out the constants to simplify the integral if you want.) \begin{align*} \vec{E} &= \vec{E}_{+Q}+\vec{E}_{-Q} \\ &= \int_0^L\frac{1}{4\pi\epsilon_0}\frac{Q\text{d}y}{L\cdot|r_x\hat{x}+(r_y-y)\hat{y}|^3}(r_x\hat{x}+(r_y-y)\hat{y}) + \int_0^L\frac{1}{4\pi\epsilon_0}\frac{-Q\text{d}x}{L\cdot|(r_x-x)\hat{x}+r_y\hat{y}|^3}((r_x-x)\hat{x}+r_y\hat{y}) \\ &= \frac{Q}{4\pi\epsilon_0L}\left(\int_0^L\frac{\text{d}y}{|r_x\hat{x}+(r_y-y)\hat{y}|^3}(r_x\hat{x}+(r_y-y)\hat{y}) - \int_0^L\frac{\text{d}x}{|(r_x-x)\hat{x}+r_y\hat{y}|^3}((r_x-x)\hat{x}+r_y\hat{y})\right) \\ \end{align*} At this point we have the integrals set up, which you could solve by hand if you so desire or plug them into Wolfram Alpha, Mathematica, or some other computation program.