Return to Capacitors in Circuit
Finding the Capacitance of a Cylindrical Capacitor
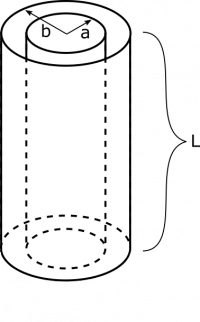
Find the capacitance of a cylindrical capacitor. The structure of the capacitor is a cylindrical shell inside another cylindrical shell. The two shells become oppositely charged when the capacitor is connected to a power source. The length of the cylinders is $L$, and their radii are $a$ and $b$, with $a<b$.
Facts
- The length is $L$
- The inner radius is $a$, and the outer radius is $b$.
- The two cylinders are shells, so all charge will accumulate on the surface.
Lacking
- Capacitance
Representations
- We represent capacitance as $$C=\frac{Q}{\Delta V},$$ where $Q$ is the charge on one of the capacitor's conductors (cylinders, in this case), and $\Delta V$ is the potential difference between them.
- We represent the situation below.
Solution
In order to find capacitance, we need a charge $Q$ and a potential difference $\Delta V$. But the potential difference depends on how much charge is on the cylindrical plates. The idea here is to use the charge that is on the plates and use that charge to then solve for $\Delta V$. When we compute the capacitance, the charge on the plates should cancel out so that the capacitance only depends on the shape/size of the cylinders. For now, we say there is a charge $Q$ on the inner cylinder, and a charge $-Q$ on the outer cylinder. Since the cylinders are conductors (as they would be in any capacitor), the charge is uniformly distributed on the cylindrical shells.
In order to arrive at potential difference, we will need to find the electric field. Remember from the notes on electric potential that in general we can write the expression for potential difference as $$\Delta V=V_f-V_i=-\int_{r_i}^{r_f} \vec{E}\bullet \text{d}\vec{r}$$
We will end up integrating in the radial direction (a convenient choice, as this is how the electric field is directed!) from $a$ to $b$, which will give us the potential difference between the two cylinders.
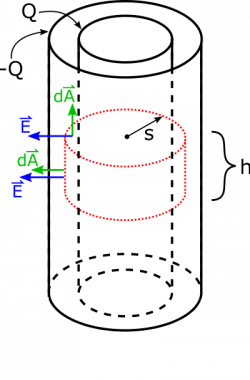
In order to find the electric field between the cylinders, we will use Gauss' Law. Below, we show a Gaussian surface that is cylindrical and fits inside the capacitor, with a radius $s$, which $a<s<b$. We also show vectors for area and electric field for the top and wall of the cylinder.
We have done a similar problem involving Gauss's Law before. In order to find the electric flux in terms of the electric field, we write $$\Phi=\int\vec{E}\bullet \text{d}\vec{A}$$
The integral is over the entire Gaussian surface, upon which $\vec{E}\bullet \text{d}\vec{A}$ takes on different values. On the top and bottom of the Gaussian surface, the electric field is directed radially, whereas the area-vectors point up and down, respectively (as shown above). Both cases yield $\vec{E}\bullet \text{d}\vec{A}=0$, so we can safely ignore this part of the integral. On the wall of the Gaussian surface, the electric field and the area-vectors are both directed radially, so their dot product simplifies to $$\vec{E}\bullet \text{d}\vec{A} = E(s)\text{d}A$$
We write $E(s)$ because the electric field magnitude depends only on the distance from the central vertical axis. Note, this notation is read as “electric field as a function of s” and NOT as “electric field times s”. Another way to think about this is to say we can rotate the entire system about this axis and it does not change, so $E$ cannot depend on the angle $\phi$. We can also shift the entire system up or down along the axis, and it does not change (using the “$L$ is very large” assumption), so $E$ cannot depend on $z$. All that remains is $r$ or how far away you are from the cylinder. And since all along the Gaussian surface, $r=s$, we write $E(s)$.
At this point, we can apply Gauss' Law. We equate flux to the charge enclosed divided by $\epsilon_0$: \begin{align*} \frac{Q_{enclosed}}{\epsilon_0} &= \int\vec{E}\bullet \text{d}\vec{A} \\ &= \int E(s)\text{d}A \\ &= E(s) \int \text{d}A \\ &= E(s) A_{wall} \\ &= E(s) (2\pi sh) \end{align*}
Approximations & Assumptions
In order to take the electric field term out of the integral there are two assumptions that must be made.
- The charge is uniformly distributed amongst the cylindrical plates: Any charge concentrations would create inconsistencies in the electric field from the charges cylinders. This is a good assumption for highly conductive plate materials.
- The length of the cylinders is much greater than how far they are apart: This allows the electric field to be constant along the length of the cylinder at a given radius so long as the last assumption also holds.
The last thing we need is $Q_{enclosed}$. This is simply the fraction of $Q$ that the Gaussian surface encloses. Since the height of the Gaussian cylinder is $h$, we have $Q_{enclosed}=\frac{h}{L}Q$. We can now write the magnitude of the electric field at a radius $s$ from the central vertical axis (given that $a<s<b$). $$E(s)=\frac{Q_{enclosed}}{\epsilon_0}\frac{1}{2\pi sh} = \frac{Q}{2\pi\epsilon_0 L s}$$
This is the magnitude of the electric field between the conducting cylinders. We can now find the potential difference between the plates. Notice below that we simplify the dot product in the same way we simplified the flux through the wall of the Gaussian surface. \begin{align*} |\Delta V| &= \int_{r_i}^{r_f} \vec{E}\bullet \text{d}\vec{r} \\ &= \int_a^b E(s)\text{d}s \\ &= \frac{Q}{2\pi\epsilon_0 L} \int_a^b \frac{1}{s}\text{d}s \\ &= \left. \frac{Q}{2\pi\epsilon_0 L} \log (s)\right|_{s=a}^{s=b} \\ &= \frac{Q}{2\pi\epsilon_0 L}\log\left(\frac{b}{a}\right) \end{align*}
Finally, we can find the capacitance based on the charge of one cylinder and the potential we just found: $$C=\frac{Q}{\Delta V} = \frac{2\pi\epsilon_0 L}{\log\left(\frac{b}{a}\right)}$$ Notice that the capacitance no longer depends on the charge Q, but only on the shape/size of our capacitor ($a$, $b$, and $L$ )