Motivating Ampere's Law

So far in this course, we have talked about the sources of electric fields, how electric fields are applied to circuits, and the sources of magnetic fields. Over the next two weeks, we are going to talk about two mathematical shortcuts for calculating the electric and magnetic fields: Ampere's Law and Gauss's Law. In both Ampere's Law and Gauss's Law, we will require that either the magnetic field (for Ampere's Law) or the electric field (for Gauss's Law) be highly symmetric. We'll start by talking about Ampere's Law, which is an alternative method for calculating the magnetic field (though there will be many parallels between Ampere's Law and Gauss's Law). Next week we will learn about Gauss's Law, the electric field equivalent of Ampere's Law.

Last week when solving for the magnetic field from a current, we used an integral (and superposition) to add up the magnetic field from the current in each little chunk of wire, which we called the Biot-Savart Law. The Biot-Savart law is always true, but the integral can sometimes be impossible to solve by hand. In these cases, you can always program the computer to do the superposition for you - the computer is very good at repeatedly adding many little bits of something!

Where Biot-Savart becomes a bit unwieldy is when we want to find the magnetic field due to distributions of currents (termed volume currents) where the symmetry is really simple (e.g., a long thick wire with current throughout). In this case, we will find that Ampere's Law is a nice shortcut to solving these problems. So think of Ampere's Law as a useful analytical technique that can be used in some cases where the symmetry of the situation (as we will see) suggests it's a better choice than Biot-Savart. Ultimately both give you the magnetic field at a location, but sometimes one approach makes the math a bit easier.

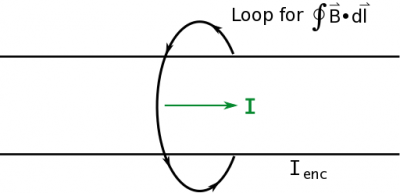
So then, what is Ampere's Law? Ampere's law (at it's most fundamental) is a way to relate the magnetic field ($\vec{B}$) to the source of the field (i.e., moving charges, $I$). In equation form, Ampere's Law is given by:

$$\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}$$

This equation says that if we add up little bits of the magnetic field along the length of any closed path (the $\oint \vec{B} \cdot d\vec{l}$ part) that should be related to the amount of current that passes through this closed path (the $\mu_0 I_{enc}$ part). This equation is true for any closed path around a current, but we will see that there are some choices of path that are easier to handle mathematically than others. (This is the main reason why we need very symmetric fields to be able to use Ampere's Law.) Because we get to choose the closed path, we will often refer to this path as an “imagined loop” or an “Amperian loop”.

The next few pages of notes will unpack each of the parts of this equation and show how we can use it to find the magnetic field from a current.