Summary of Electricity and Magnetism (thus far)
So far in this course we have primarily talked about static electric fields (Weeks 1 - 3), how static electric fields apply to circuits (Weeks 4 - 6), and static magnetic fields (Weeks 7 - 9). We have primarily been treating these phenomena as independent (i.e. only looking at the electric field or only looking at the magnetic field). However, as you may have guessed, these ideas are not completely separate. For example, let's say that you had a positive charge moving down and a negative charge moving up. There would be an electric force from the negative charge on the positive charge. However, there would ALSO be a magnetic force from the negative charge on the positive charge because the positive charge is moving through the magnetic field produced by the negative charge.
Now that we have the basics down for both electric and magnetic fields, we will start to consider the cases where charges feel an effect from both electric and magnetic interactions. (We will also return to this idea again at the end of the course.) This page of notes serves as a reminder of some of the important concepts about static electric fields and static magnetic fields that we will be building on for the rest of the semester.
Static Electric Fields
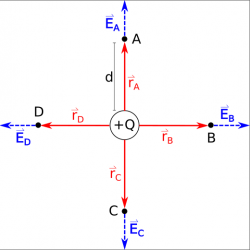
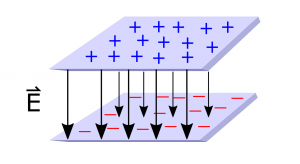
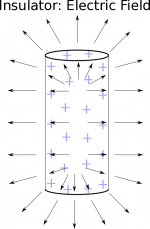
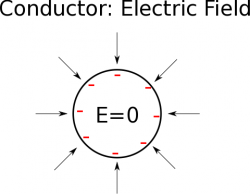
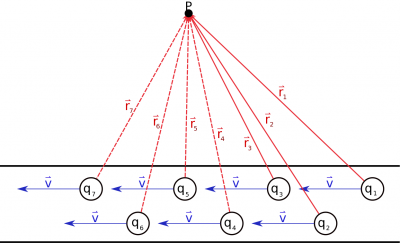
In the beginning of the semester, we talked about how electric charges created electric fields. We talked specifically about the electric field from point charges which points radially outwards for positive charges (or radially inward for negative charges). We then used both computational methods (VPython code) and analytical methods (integration) to find the electric field for lines of charge, planes of charge, and volumes of charge (cylinders and spheres). In each of these cases, we found that the electric field would still point away from positive charges and toward negative charges.
The electric force was then defined by how a charge would interact with an electric field: →FE=q→E. Because the charge is a scalar value, the electric force will always point either in the same direction as the electric field (for positive charges) or opposite the electric field (for negative charges), which will cause the charge to accelerate. Since the path that the charges follow is in the same direction as the electric force, we can relate the electric force to a change in electric potential energy or to a change in electric potential.
Static Magnetic Fields
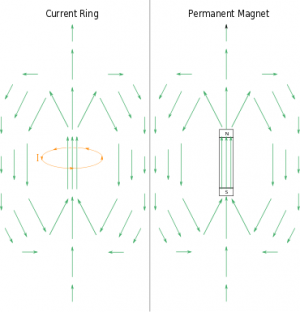
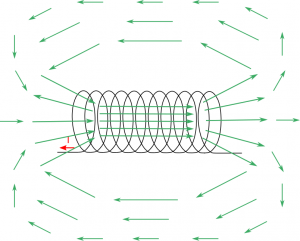
In contrast to electric fields, we found that a moving charge created a magnetic field that was perpendicular to motion of the moving charge. This meant that the magnetic field pointed circularly around a moving charge, which we were able to determine using the right hand rule. Again, we used computational and analytical methods to show that the magnetic field from a current also followed a similar pattern. From these basic sources, we could then extend to the magnetic field from current loops, from bar magnets, and (briefly) from solenoids.
The magnetic force was then defined as the interaction between a charge and a magnetic field: either →FB=q→v×→B or →FB=∫Id→l×→B - depending on if we were examining the force on a point charge or the force on a current wire. In both of these cases the magnetic force was perpendicular to the motion of the particles and perpendicular to the magnetic field because of the cross product. Since the magnetic force is always perpendicular to the motion of the particles, this means that the magnetic force only changes the direction of the particle's velocity - it does not speed the particle up or slow the particle down.