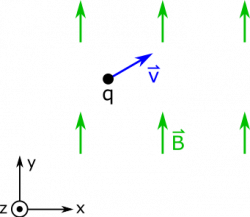
Suppose you have a moving charge $q=20 \text{ mC}$ in a magnetic field $\vec{B} = 15 \text{ mT } \hat{y}$. The charge has a velocity of $\vec{v} = (3\hat{x} + 2\hat{y}) \text{ m/s}$, and a mass of $m = 1 \text{ g}$. What does the motion of the charge look like?

• There is a charge $q = 20 \text{ mC}$.
• The charge has velocity $\vec{v} = (3\hat{x} + 2\hat{y}) \text{ m/s}$.
• The charge has a mass $m = 1 \text{ g}$.
• The charge is in a field $\vec{B} = 15 \text{ mT } \hat{y}$.

• The motion of the charge.

• The B-field is constant.
• Charge and Mass of the particle are constant.

• We represent the magnetic force on a moving charge as

$$\vec{F}= q \vec{v} \times \vec{B}$$

• We represent the situation below.

Moving Charge in a Magnetic Field

We can recall an earlier example where we had to find the motion of a charge in a magnetic field. Based on that example, if our particle were moving in the $\hat{x}$ direction, then the $\hat{y}$-directed magnetic field would cause circular motion in the $xz$-plane. The radius of this motion would be, as before, $$r = \frac{mv}{qB}$$

However, in this example the motion of the particle is a little different. There is a $\hat{y}$ component to the velocity, which is parallel to the magnetic field – to be clear, the velocity as a whole is not parallel to the magnetic field, but the existence of the $\hat{y}$ component guarantees that they are not perpendicular. Because the magnetic field is directed completely in the $\hat{y}$-direction, we know that $\vec{v}\times\vec{B}$ will always be perpendicular to the $\hat{y}$-direction. In connection with this, since $\vec{F}= q \vec{v} \times \vec{B}$, this means that the $\hat{y}$ component of the force is zero, $F_y = 0$. Since the particle never experiences a force in the $\hat{y}$-direction, the $\hat{y}$ component of the velocity will never change.

So it seems like the motion here will not be circular. The magnetic force still plays a role, though because the velocity also has an x-component. From the magnetic force equation, we find that the magnetic force would be: $$\vec{F}= q \vec{v} \times \vec{B} = = q (v_x \hat{x} + v_y \hat{y}) \times (B \hat{y}) = q v_x B \hat{z}$$

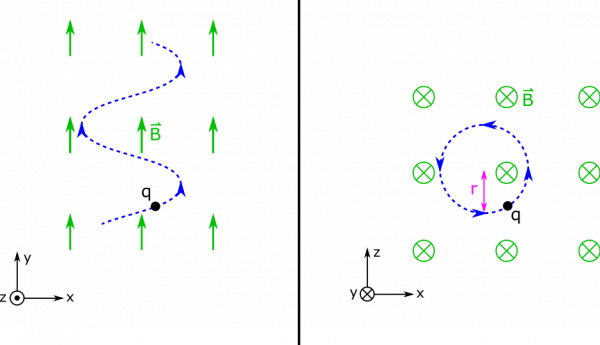
This force would still push the particle into a circular motion (while still not affecting the particle's motion in the y-direction.) So the particle would move in an upwards spiraling path.

So when we look at the motion of the particle from the perspective of $+y$ going into the page, we should see a circle with radius $$r = \frac{mv_x}{qB} = 10 \text{ m}$$

However, because of the constant $\hat{y}$ component of the velocity, this circle is actually a helix. Two perspectives show the motion below.

Motion of the Moving Charge