Return to resistors and conductivity
Example: Application of Ohm's Law
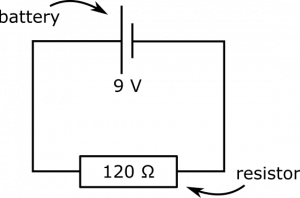
Suppose you have a simple circuit that contains only a 9-Volt battery and a resistor of $120 \Omega$. What is the current in the wire?
Facts
- $\Delta V = 9\text{ V}$
- $R = 120 \Omega$
Lacking
- Current
Approximations & Assumptions
- The wire has very very small resistance when compared to the 120 $\Omega$ resistor.
- The circuit is in a steady state.
- Approximating the battery as a mechanical battery.
- There is no outside influence on the circuit.
Representations
- We represent Ohm's Law as $\Delta V = IR$.
- We represent the situation with following circuit diagram.
Solution
We have assumed that the battery and the wire contribute negligible resistance to the circuit. So the resistance of the circuit is simply the resistance of the resistor: $R = 120\Omega$. These assumptions also lead us to conclude that the voltage that is provided by the battery is used up only in the resistor (and not on the wires). So the potential difference across the resistor is the entire 9 Volts, so $\Delta V = 9 \text{ V}$. We can now use Ohm's Law to find the current through the circuit: $$I = \frac{\Delta V}{R} = 75 \text{ mA}$$