Section 19.2 in Matter and Interactions (4th edition)
Resistors and Conductivity
So far we have been approaching circuits from a very microscopic picture, including talking about the surface charges, electron currents, and electric fields in the wires. However, the surface charges, electric fields, and individual electrons are extremely difficult to measure. Instead, it often much more useful to think about circuits in terms of macroscopic properties, which are much easier to measure (i.e., conventional current instead of electron current or potential difference instead of electric field). These notes will start to connect the microscopic features of circuits that we have been talking about to the macroscopic measures.
Conductivity
Conductivity is a way to relate the properties of the materials (like electron density and electron mobility), the electric field, and the conventional current. Remember from before, that we defined the conventional current (I) to be the electron current (i - number of electrons per second passing a point in the circuit) times the magnitude of one of the moving charges (|q|). I=|q|i
Typically, we will group together the properties that come from the material (q, n, and u) into a single property called conductivity. Conductivity is represented by a σ where σ=qnu
This could also be written in terms of the current density: J=IA=σE
Because electric field is a vector, we can consider current density to be a vector that points in the direction of the conventional current, which points in the same direction as the electric field in circuit. →J=σ→E
Resistance
Before when we talked about resistors, we said that a resistor was a section or part of the circuit where the passage of electrons requires more energy (conventionally, that it resists the passage of electrons more than other parts of the circuit). We found there to be a larger electric field, a larger drift velocity, and a larger surface charge gradient over the resistor. Resistance is a way to quantify how much a resistor resists the passage of electrons based off the properties of the material (electron mobility and electron density) and the shape of the resistor.
Derivation of R
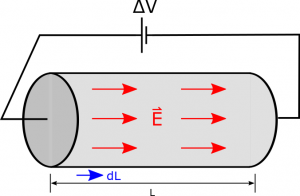
For example, suppose we have a resistor that has a cross sectional area of A, a length L, and a potential difference of ΔV from one end to the other. If we assume a steady state current, then the electric field inside the resistor would be constant in magnitude and direction and would point along the length of the wire. We could use the relationship between electric potential and electric field then to write: ΔV=−∫fi→E⋅→dl
Because →E would point along the length of the wire, we would want to integrate along the length of the wire, which would mean that →E and →dl would be parallel. This simplifies the dot product to just a multiplication, leaving: |ΔV|=∫L0Edl
If we solve for the conventional current, and do some rearranging of the (σA) using fractions we would get: I=ΔVLσA
Making sense of R
Why does the bottom fraction make sense? A longer, thinner wire should be more resistive, so the geometric properties make sense (directly proportionally to L and inversely proportional to A). A wire with higher conductivity should be less resistive, which also make sense (inversely proprtional to σ).
Resistance has units of volts per amp, which is also called an ohm. An ohm is represented by a capital omega (Ω). Sometimes you may see resistance rewritten in terms of resistivity(ρ), which is simply the inverse of conductivity ρ=1/σ. So using resistivity, R=ρLA - either version of resistance is fine.
Ohm's Model
Perhaps equally as important, we can now relate the change in electric potential over a resistor to the resistance and current passing through the resistor. This model of resistance works well for low voltage and currents. This model is also often called “Ohm's Law”: ΔV=IR
Summary
To summarize, we can compare the microscopic and macroscopic views of circuits. In the microscopic view, we write the average drift velocity of the electrons in terms of the electron mobility and the electric field. In the macroscopic view, instead we write the current density in terms of the conductivity and the electric field. In the microscopic view, we tend to talk about the electron current in terms of the electron density, electron mobility, area of the wire, and electric field; whereas, in the macroscopic view, we talk about conventional current in terms of the potential difference and resistance.
| Micro | Macro |
|---|---|
| vavg=uE | J=σE |
| i=nAvavg=nAuE | I=|q|i=ΔVR |