Section 21.6 in Matter and Interactions (4th edition)
Magnetic field along a closed loop
For the context of our explanation, we will use a long straight wire with a current $I$ running through it as our example. We'll start by talking about a thin wire and eventually build up to talking about a thick wire. In this class, we will also make the typical assumption that the current in the wire is uniform and in a steady state (upper-division courses may address non-uniform currents). That is, at every point in the wire the same amount of charge per unit time exists.
What is the "shape" of the magnetic field?
Since we already calculated the B-field from a long straight wire using the Biot-Savart law (by adding up all the contributions), we already have some insight into to what we think the magnetic field should be from the wire - it should curl around the wire. (We will eventually use the Biot-Savart result at the end to verify what we find using Ampere's Law.) For Ampere's Law, the structure, shape, and symmetry of the magnetic field is very important to understanding how to set up the different parts of the equation. This means that the first step in Ampere's law is to draw the magnetic field.
Magnetic field circulates around moving charges
As you have seen before, the magnetic field circulates around a moving charge. Below is a simulation that shows this for a series of moving point charges.
As you can see, the sizes of the magnetic field vectors (the arrows) get larger as the charges get closer to the observation locations and get smaller as they pass and move away. The direction of the magnetic field is always around the path of the charges. Now, imagine a constant stream of particles very close together, that is, a current of many electrons moving in a wire. In that case, the direction of the magnetic field is still around the wire, but the magnitude stays constant. That is, for a steady current, the magnetic field at any one point is a constant in time. Furthermore, for cylindrical wires (the ones we will focus on), the magnitude of magnetic field is constant for a given distance from the wire. You saw this with the long wire when we solved the problem using Biot-Savart.
Symmetry is critical
The structure (or symmetry) of this field is very useful for Ampere's Law. That is, the fact that the B-field always circulates around the wire and is the same magnitude for a given distance makes this problem of a steady state current an excellent candidate for using Ampere's Law. In fact, this symmetry holds inside the wire as well. That is, there will be a constant magnitude magnetic field circulating around every point inside the wire as well! This is a really important result that we can explore with Ampere's Law, but that can be a real challenge to deal with using Biot-Savart.
We'll start by thinking about the magnetic field outside a wire and the mathematical representation Ampere's Law:
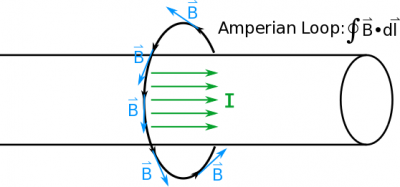
$$\oint \vec{B} \bullet d\vec{l} = \mu_0 I_{enc}$$
Again, the first thing we will consider will be the shape of the magnetic field for the situation - which is related to the left-hand side of Ampere's Law - namely the $\oint \vec{B} \bullet d\vec{l}$ part.
What is $\vec{B}\bullet d\vec{l}$?
You have seen these kinds of dot products before - when we defined electric potential. But in the case of electric potential, we understood this to be a measure of work per unit charge. In the case of the magnetic field, there is no such analog. That integral of the magnetic field along a path is not the considered “work”. As you saw before, the magnetic force has important properties that make it such that the magnetic field cannot do work. So what is this $\vec{B}\bullet d\vec{l}$ thing?
This integral formulation comes from the mathematical model that the magnetic field seems to obey in every instance we observe it. Namely, how much the magnetic field curls around the wire depends on how much current there is creating the magnetic field. This measure, which is beyond the scope of this course, called the curl of the magnetic field is an important property of the field and is an essential quality of what distinguishes it from the electric field (a single stationary charge has an E-field that points away or towards the charge - it cannot be curly).
So think of $\vec{B}\bullet d\vec{l}$ as the little measure of how much the magnetic field curls around its source (the current). Our job is to add up all those little contributions along a closed path to find the curl of the magnetic field at a given distance from the current,
$$\oint \vec{B} \bullet d\vec{l}.$$
This gives us the full left-hand side of the equation, it is measure of how curly the magnetic field is at some distance from the current.
How do we compute it?
First, we want to pick a Amperian loop (or the imaginary path) so that the observation point is somewhere along the path. For example, if we wanted to find the magnetic field a distance of $R$ away from the wire, we would want to pick a loop that has a radius of $R$ around the wire.
Then, since we get to pick what kind of loop we want, we want to choose a loop that will make our math easy. If we look at the $$\oint \vec{B} \bullet d\vec{l}$$ - there are a couple of steps that will make our calculation MUCH simpler:
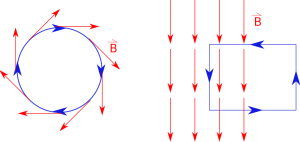
- We want $\vec{B}$ to be parallel to $d\vec{l}$ because then the dot product turns into multiplication $$\oint \vec{B} \bullet d\vec{l} = \oint |\vec{B}||d\vec{l}| $$
- We want the magnitude of $\vec{B}$ to be constant so we can pull it out of the integral $$\oint |\vec{B}||d\vec{l}| = |\vec{B}| \oint |dl|$$
This means we want to choose a closed loop that: 1) is always following the B-Field (to make $d\vec{l}$ parallel to $\vec{B}$) and 2) has a constant B-Field everywhere around the loop. So if the magnetic field points in circle around the wire, you want to pick a circular loop. If the magnetic field is constant, you want to pick a loop with at least one straight edge (like a rectangular loop).
It's important to note that this loop isn't real - there is not a wire or anything physically around the wire. It's an imagined loop that helps guide our work with Ampere's Law. We refer to this imagined loop as the “Amperian Loop.”
Formally, we are doing a path or line integral around a loop with the magnetic field, but for most cases this integral will simplify quite a bit. Also, it's ok if this idea is a bit abstract now, we will put it all together with an example in next set of notes.
Long Wire Example
Both of these conditions are satisfied if we pick a circular Amperian loop that is centered on a wire with a uniform distribution of current: 1) the magnetic field points in the same direction as our Amperian loop and 2) it has the same magnitude along that loop. This makes the calculation of this integral is relatively straight-forward.
For an Amperian loop of radius $R$ centered on a wire with uniform current, we find that this integral is,
\begin{align*} \oint \vec{B} \bullet d\vec{l} &= \oint |\vec{B}||d\vec{l}| \\ &= \oint B dl \\ &= B \oint dl \\ &= B l \end{align*}
where the first two steps listed come from the fact that $\vec{B}$ points in the direction of $d\vec{l}$ everywhere on the loop (so the dot product simplifies to multiplication) and the last two steps listed come from the fact that the B-field is the same magnitude along that loop (so you can pull it out of the integral). The resulting integral of $dl$ gives just $l$. Because this length comes from the integration of the $dl$, the length $l$ here represents the length of the Amperian loop. For our example, the length of the loop would just be the circumference of the loop. Since we said that the loop would have a radius R, this means $l=2\pi R$, so we get: $$\oint \vec{B} \bullet d\vec{l} = B(2 \pi R)$$
Remember that the $B$ in this equation is the magnitude of the B-field on that loop (so this would be the magnetic field at a distance $R$ away from the straight wire).