Section 21.1 from Matter and Interactions (4th edition)
Enclosed Charge
One of the coolest, yet strangest, features of Gauss's Law is that the electric flux through the imagined Gaussian surface is related to the total amount of charge inside the surface (the “enclosed charge”). For a point charge or multiple point charges, it is fairly easy to find the total amount of enclosed charge - you simply sum the amount of charge that is inside the surface you picked. However, if you have a line, sheet, or volume of charge, we need to rely on charge density to find the enclosed charge. These notes will review charge density and show how we find the enclosed charge for various shapes or distributions of charge.
Charge Density and Charge
We have talked about charge density in terms of finding a dQ, where we assumed a uniform (or constant) charge density. We will make that same assumption again here (the more complicated non-uniform charge densities may be covered in upper division courses). For a uniform charge distribution, the charge density tells you how much charge there is per unit length (for 1D lines of charge), per area (for 2D sheets of charge), or per volume (for 3D shapes of charge). For 1D charge distributions, we use λ as the charge density (which has units of C/m); for 2D charge distributions, we use σ as the charge distribution (which has units of C/m2); and for 3D charge distributions, we use ρ as the charge density (which has units of C/m3).
If we know the total charge and the total length/area/volume, we can calculate the charge density using: λ=QtotLtotσ=QtotAtotρ=QtotVtot
The charge density then can be used to figure out how much charge is in a certain amount of length, area, or volume, depending on what kind of charge you have: Q=λL=QtotLtotLQ=σA=QtotAtotAQ=ρV=QtotVtotV
As an example, say you have charged a 20 cm piece of tape so it has a charge density of λ=4.9∗10−7C/m. To find the amount of charge in the bottom 5 cm of tape, you would take: Q=λL
Or similarly, to find the total amount of charge in the piece of tape: Qtot=λLtot
We will use this method to find how much charge is enclosed by the Gaussian surface when solving for the electric field or electric flux.
Patterns of Electric Fields
For Gauss's Law to be easily solvable, we rely heavily on symmetry, which limits our choice of charge distribution to three general shapes: spheres (or points) of charge, lines or cylinders of charge, and plates of charge.
Spheres of Charge
For a sphere of charge, (much like a point charge), the electric field vectors point radially away (for positive charge) or radially toward (for negative charge) the sphere. Since the electric field vectors point radially, we would want to choose a sphere as a Gaussian surface to enclose the charge because the →dA's at every point along the sphere would also point radially outward. Choosing a sphere as the Gaussian surface then means that the electric field vector and the dA vector are always parallel or antiparallel, which helps us simplify the electric flux integral.
Lines or Cylinders of Charge
In the middle of a line (1D) or cylinder of charge (3D), the electric field vectors point radially away from a line of positive charge or radially toward a line of negative charge. If we make the line extremely long or zoom in to focus on a very small portion of the line/cylinder near the middle, the electric field vectors will point perpendicular to the surface. When dealing with lines or cylinders, we will often ignore the electric field near the ends because in that case the field vectors are not constant in magnitude or direction (which is much harder to deal with mathematically). Thus, we will often assume that the line/cylinder is extremely (or infinitely) long or that we only care about the middle section where the electric field is constant.
If we wanted to find the electric field from a very long line or cylinder of charge, then we would want to choose a (smaller) cylinder as the Gaussian surface around the line/cylinder of charge because the electric field vectors would then point in the same radial direction as the dA vectors. In the next page of notes, we talk about the cylinder example in more detail.
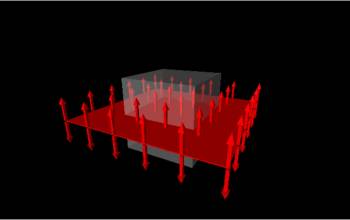
Sheets of charge
Similar to the lines of charge, the electric field for a positive plate of charge points perpendicularly away (and perpendicularly toward the plate for negative charge) in the middle of the plate. Near the edges of the plate (similar to the line of charge) the electric field vectors change directions and magnitudes, making it much harder calculate. Typically, we will make the assumption that the charged plate is very large (or infinite) or that we only care about the field close to the center of the plate away from the edges.
If we wanted to find the electric field from a large plate of charge, then we would want to choose a (smaller) cylinder or rectangular prism as the Gaussian surface around the plate of charge because the electric field vectors would then point parallel to the dA vectors through the top and bottom surfaces.
Examples
-
- Video Example: Flux through a Cylinder on a Line of Charge